Greens formel - fel svar (2)

Till att börja med är jag fundersam på din nämnare:

$x^2+y^2-2x-2y+2 = (x-1)^2+(y-1)^2$

Sedan har du korrekt att $\displaystyle \frac{\partial Q }{\partial x}-\frac{\partial P }{\partial y} = 0$ och vi får med Greens formel att linjeintegralen över det slutna området är noll. Det du gör sedan är jag inte helt hundra på men det bör stämma.

Fixa till din nämnare bara så blir det säkert bra.

Tillägg: 27 sep 2021 21:49

Å andra sidan, Greens formel gäller inte om det finns en singularitet i området vilket det finns i detta fall (1,1).

Men den här uppgiften ska lösas med Greens formel då den ingår i övningarna till det kapitlet.

Tillägg: 27 sep 2021 21:59

Jag ändrar nämnaten pch får fel svar ändå. :(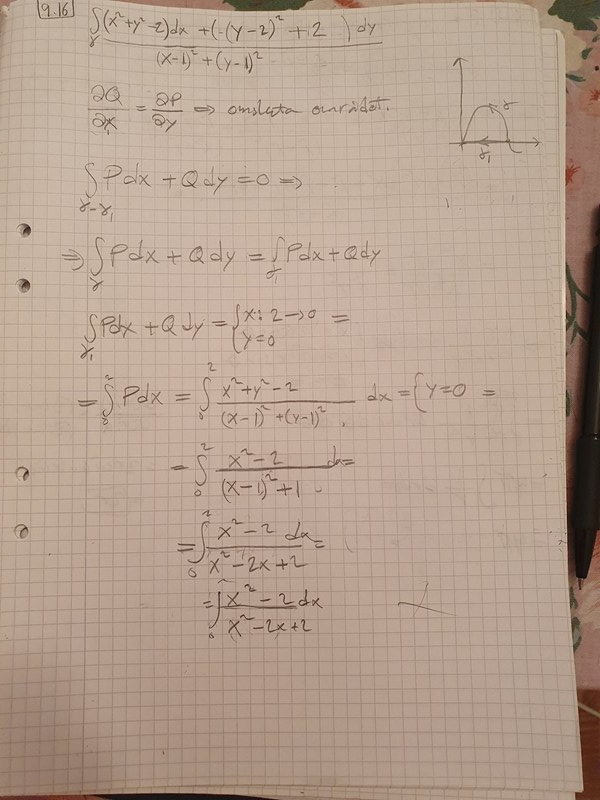

Du har sjabblat till täljaren också:

$P = x^2+y^2-2$

$Q = 4y-x^2-y^2-2 \neq -(y-2)^2+2 =4y -y^2-2$

Tenta snart?

Ebola skrev:

Du har sjabblat till täljaren också:

$P = x^2+y^2-2$

$Q = 4y-x^2-y^2-2 \neq -(y-2)^2+2 =4y -y^2-2$

Omg..

Tenta snart?

Haha nej, men läggdags är det.

Tillägg: 27 sep 2021 22:16

Ps. Jag använder dock inte Q i beräkningarna  😬😬

Det har du rätt i. Svaret blir oavsett $\pi - 2$, vad ska det bli enligt facit?

Det som sker när du har en singularitet i området är normalt att även om curl för vektorfältet är noll är inte vektorfältet konservativt och du kan inte tillämpa Greens formel så som du gjorde.

Att $\nabla \times \vec{F}=0$ är nämligen inte ett tillräckligt krav för att vektorfältet ska vara konservativt. Det ska också vara vägoberoende. Man brukar kontrollera detta med en cirkel runt singulariteten har jag för mig.

Hur gör man för att använda Greens sats då? Med singularitet menar du att integranden inte är definierad i (1,1)?

Att övningen finns i ett kapitel som handlar om Greens formel betyder inte att du måste använda Greens formel för att lösa uppgiften. Övningen kan lika gärna finnas där som ett exempel på när Greens formel inte är tillämplig.

I vilket fall bör du alltid lösa uppgifter med den metod du tycker är enklast.