Gränsvärdena för theta till en dubbelintegral, polära koordinater.
Detta är ingen uppgift som finns i min bok eller så utan något jag funderat över.
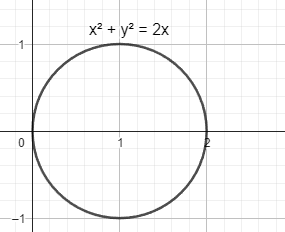
Låt oss säga att vi vill beräkna arean av cirkeln m.h.a en dubbelintegral. Jag undrar hur tänket går när man får gränsvärdena till -integralen. Min första tanke var att men det verkar vara fel.
(Det går att beräkna arean i polära koordinater med centrum i origo, men det finns lättare sätt.)
Då cirkeln befinner sig i högra halvplanet så kommer theta (med den vanliga definitionen) att anta värden mellan t.ex -pi/2 och pi/2.
(Ta en punkt på kurvan och rita ut r och theta.)
Dr. G skrev:(Ta en punkt på kurvan och rita ut r och theta.)
Ok jag tror att jag började räkna theta från centrum på cirkeln, men att jag egentligen bör gå från origo?
Dr. G skrev:(Det går att beräkna arean i polära koordinater med centrum i origo, men det finns lättare sätt.)
Då cirkeln befinner sig i högra halvplanet så kommer theta (med den vanliga definitionen) att anta värden mellan t.ex -pi/2 och pi/2.
(Ta en punkt på kurvan och rita ut r och theta.)
Vi har att så om vi tar säg som är inom intervallet du angav så får vi en punkt på den översta delen av cirkeln men vi får aldrig någon punkt på den undre delen? Är inte detta intervallet felaktigt då? Måste vara
Den gröna vinkeln är positiv och den röda är negativ. Punkten på kurvan närmar sig origo när vinkeln går mot ±pi/2. 
Dr. G skrev:Den gröna vinkeln är positiv och den röda är negativ. Punkten på kurvan närmar sig origo när vinkeln går mot ±pi/2.
Tack så mycket! Eftersom vi har symmetri i x-axeln skulle vi lika gärna kunnat ta och multiplicerat integralen med 2?
Ja, du kan även titta på integranden och se att du har en jämn funktion på ett symmetriskt intervall.
(integral från -a till a) är då samma sak som 2*(integral från 0 till a).


