Gränsvärden flervariabel
Hej, behöver lite hjälp med denna. Jag har testat att närma mig (0,0) längst ett antal linjer och det verkar som hur jag än försöker närma mig (0,0) så får jag alltid gränsvärdet 0. Blev lite förvånad över facits lösning, förstår inte logiken i det hela. Tacksam om någon kan leda mig på rätt spår.
Om du ska visa ett gränsvärde i flervariabel så ger det INGENTING att gå längs alla räta linjer mot gränspunkten. Gränsvärdet kan saknas likafullt. Jag minns inte exemplet jag såg en gång men det var en funktion som var noll överallt utom längs en spiral in mot origo där den var 1. Då var gränsvärdet noll längs alla räta linjer men i varje liten cirkelskiva runt origo fanns det både noll och 1 som funktionsvärden.
Däremot, om du hittar två linjer med olika gränsvärden så vet du att gränsvärde saknas.
För att nu gå till exemplet:
Jag börjar med andra ledet:
x2 och y2 är ≥ 0 så y2 / (x2+y2) ≤ 1 utanför origo. |y| ≥ 0 så andra ledet är ≤ |y|
och att |y| går mot noll när vi går mot origo ligger i sakens natur.
Nu återstår att visa att första ledet är ≤ andra ledet. Om y ≥ 0 så är leden lika.
Om y < 0 så är de också lika eftersom kvoten i andra ledet inte är negativ.
Första olikheten skulle kunna vara en likhet.
Om du går över till polära koordinater så blir det i stort sett samma logik som i facit.
Mogens skrev:Om du ska visa ett gränsvärde i flervariabel så ger det INGENTING att gå längs alla räta linjer mot gränspunkten. Gränsvärdet kan saknas likafullt. Jag minns inte exemplet jag såg en gång men det var en funktion som var noll överallt utom längs en spiral in mot origo där den var 1. Då var gränsvärdet noll längs alla räta linjer men i varje liten cirkelskiva runt origo fanns det både noll och 1 som funktionsvärden.
Däremot, om du hittar två linjer med olika gränsvärden så vet du att gränsvärde saknas.
För att nu gå till exemplet:
Jag börjar med andra ledet:
x2 och y2 är ≥ 0 så y2 / (x2+y2) ≤ 1 utanför origo. |y| ≥ 0 så andra ledet är ≤ |y|
och att |y| går mot noll när vi går mot origo ligger i sakens natur.
Nu återstår att visa att första ledet är ≤ andra ledet. Om y ≥ 0 så är leden lika.
Om y < 0 så är de också lika eftersom kvoten i andra ledet inte är negativ.
Tack ska du ha. Så man ska aldrig nöja sig med att man får alla tester till 0 utan endast om man får olika svar -> gränsvärde existerar ej?
Laguna skrev:Första olikheten skulle kunna vara en likhet.
Om du går över till polära koordinater så blir det i stort sett samma logik som i facit.
Är det att föredra?
Om du förstår det bättre så är det det.
Laguna skrev:Om du förstår det bättre så är det det.
Jag läste lite om delta epsilon argument, är det bra att använda det i detta fallet?
Delta-epsilon, nja, det blir ingen skillnad, bara jobbigare. Fortfarande måste du göra samma steg i beviset.
Mogens skrev:Delta-epsilon, nja, det blir ingen skillnad, bara jobbigare. Fortfarande måste du göra samma steg i beviset.
Har en fråga. Om vi har en dubbelolikhet så typ -epsilon<f(x,y)<epsilon, får vi ändra f(x,y) hur vi vill? hur vet vi att vi inte hamnar utanför intervallet? Antar att vi endast får jobba med och inte strikta olikheter?
”Epsilon-delta” är ett sätt att Definiera gränsvärde t ex för en funktion f: Rn->Rm Det är naturligtvis en dygd att på så sätt föra bevisningen närmare axiomen. Det innebär i regel lite mer arbete, så i praktiken jobbar man ungefär som Mogens demonstrerat för dig med att ställa sig på kända satser och standardgränsvärden. Vill man fördjupa sin förståelse kan man genomföra beviset med epsilon-delta i något enstaka fall som då helst inte ska väljas bland de svåra uppgifterna. Det aktuella exemplet är alldeles utmärkt. Prova får du se och fråga om du undrar något.
Tomten skrev:”Epsilon-delta” är ett sätt att Definiera gränsvärde t ex för en funktion f: Rn->Rm Det är naturligtvis en dygd att på så sätt föra bevisningen närmare axiomen. Det innebär i regel lite mer arbete, så i praktiken jobbar man ungefär som Mogens demonstrerat för dig med att ställa sig på kända satser och standardgränsvärden. Vill man fördjupa sin förståelse kan man genomföra beviset med epsilon-delta i något enstaka fall som då helst inte ska väljas bland de svåra uppgifterna. Det aktuella exemplet är alldeles utmärkt. Prova får du se och fråga om du undrar något.
Något så här? Möjligt att jag är ute och cyklar.
Ser bra ut. Tack vare valet av ett enkelt exempel lyfter du istället fram hur epsilon och delta funkar. Hoppas det är välgörande för förståelsen. Det finns ytterligare steg att ta från epsilon-delta till ännu högre abstraktion, men den möter du nog inte ännu.
Tomten skrev:Ser bra ut. Tack vare valet av ett enkelt exempel lyfter du istället fram hur epsilon och delta funkar. Hoppas det är välgörande för förståelsen. Det finns ytterligare steg att ta från epsilon-delta till ännu högre abstraktion, men den möter du nog inte ännu.
Kul att det var rätt. Kändes väldigt tungt från början :)
Tomten skrev:Ser bra ut. Tack vare valet av ett enkelt exempel lyfter du istället fram hur epsilon och delta funkar. Hoppas det är välgörande för förståelsen. Det finns ytterligare steg att ta från epsilon-delta till ännu högre abstraktion, men den möter du nog inte ännu.
Jag försökte rita funktionen i matlab och fick ett hål vid (0,0) (den röda punkten). Försöker få bättre förståelse för vad jag gör och hur kan funktionen ha ett gränsvärde i punkten om det är ett hål?
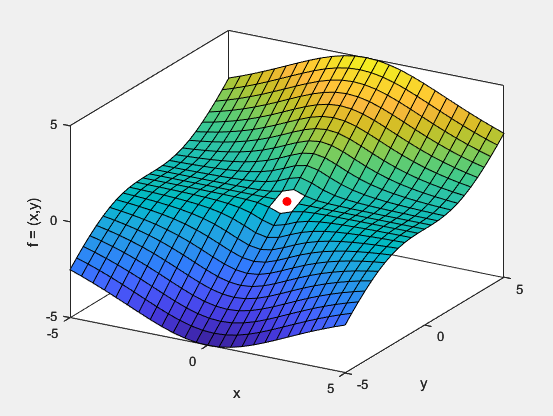
Så här ser funktionen ut i Mathematica. Det kan tyvärr hända att Matlab inte hanterar funktionen korrekt eftersom det främst är ett numeriskt verktyg. Ur Matlabs synvinkel är funktionen odefinierad i (0,0) eftersom nämnaren i uttrycket utvärderas till noll där.
Först: I alla andra punkter är det närmast ointressant att beräkna gränsvärden. Där är det bara att sätta in punkten i f(x,y)
Sedan: ”Hålet” betyder att f som den står inte är definierad i origo och därför är den inte heller kontinuerlig där. Man har rätt att själv definiera f i origo genom att helt enkelt bestämma f(0,0) = 3 t ex, men blir den kontinuerlig då? Nej, men kan man bestämma värdet så att den blir kontinuerlig? Den frågan har du redan besvarat genom att beräkna gränsvärdet. Tar matlab emot funktioner av typ f(x,y) = … för (x,y) skilt från (0,0) och f(0,0)= 0? I så fall ska hålet försvinna.
Ser nu att Daniel besvarar min fråga ovan. En gammal tomte är inte insatt i moderniteter som matlab, men kom igen med krittavla och logtabell.
D4NIEL skrev:
Jo, uttrycker ytan med en mängd punkter till (x,y,f(x,y)), så den sätter säkerligen (0,0,f(0,0)). Undrar hur jag ska göra då, aja inte så viktigt.
