Gränsvärde och derivatans definition
Har jag räknat rätt?
Är b) fel? Är gränsvärdet på a) 2x?

(a) är korrekt.
(b): Det är lite svårt att se vad du skrivit, men det är viktigt att du håller isär och funktionsuttrycket . är något annat än att sätta in istället för . :)
Här är en bättre bild:
Blir gränsvärdet 1 på grund av h/h?

Nej, inte riktigt. En bra metod för att kontrollera sitt svar i dessa fall, är att prova med deriveringsreglerna och se om du får samma svar.
Med det sagt, du blandar in funktionsuttrycket () i funktionen f. Du använder derivatans definition, och sedan byter du ut mot :
Nu kan du förenkla, så kan du sedan låta h gå mot noll och få ditt svar. :)
EDIT: Korrigerat +m till -m. :)
Jaha, just det, förlåt. Ska andra m-värdet vara positivt?
Ursäkta, lite slarv med parenteserna där. Det andra m-värdet ska vara negativt. :)
Okej, blir gränsvärdet k?
Har jag gjort rätt nu?
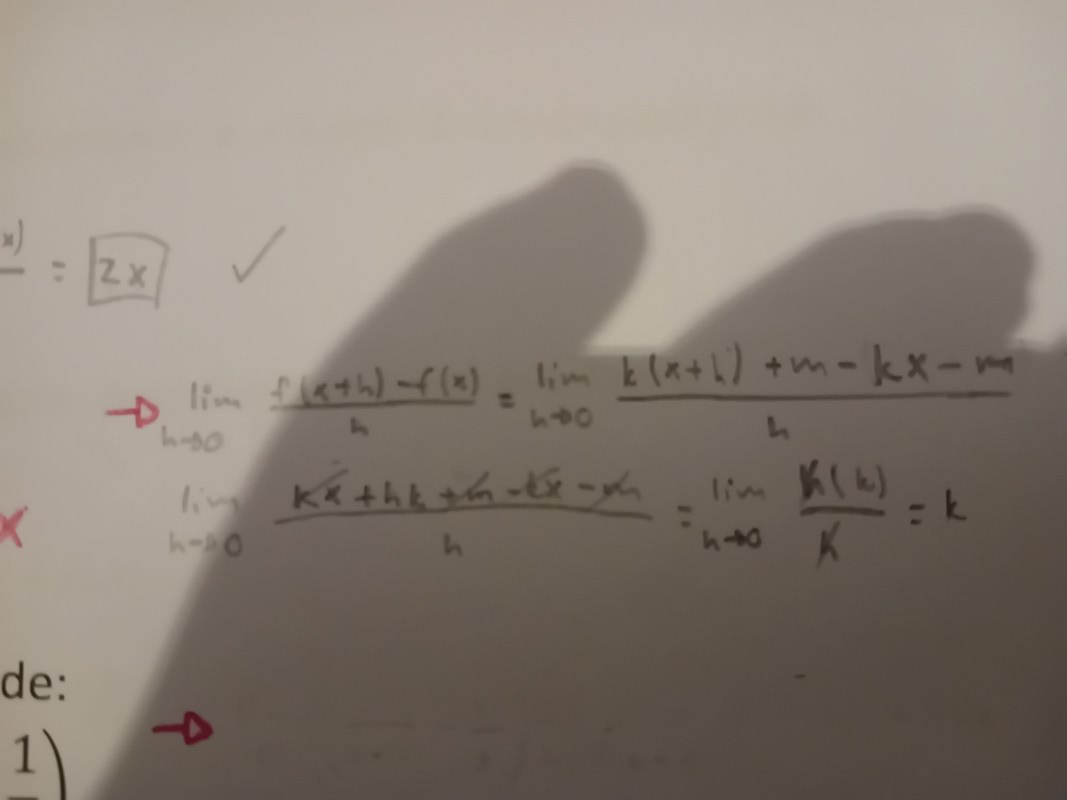
Gränsvärdet blir k, mycket riktigt!
Det ser bra ut!


