Gränsvärde med roten ur 3
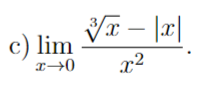
Där man ska avgöra värdet (om det existerar). I facit beräknar de enbart högergränsvärdet med motiveringen att "enligt konvention är tredje roten ur x enbart definierad för x > 0". Detta gjorde mig förvirrad! Hur ligger det till egentligen? För grafen för tredje roten ur x ser väldigt kontinuerlig ut även för negativa x. I min bok står det att "det går också att definiera a1/n för negativa a förutsatt att n är udda".
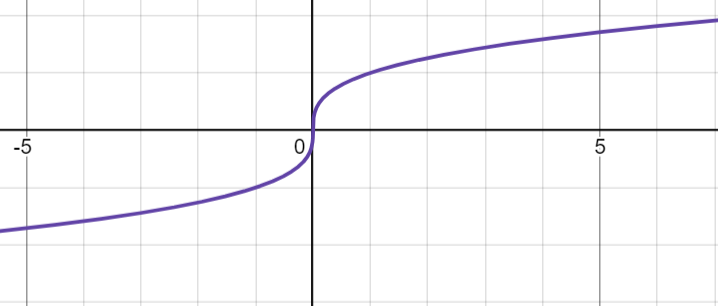
Min hypotes: tecknet roten ur är bara definierad för positiva tal, medan tecknet a1/n i vissa fall är definierat för negativa a.
En felaktig motivation. Prata med den som gjort facit.
Edit:
Notera att man kan välja principalrot enligt konvention men det är då avgörande vad man drar för slutsats av detta.
Det är ur facit till en extenta, så det som står i den borde ju vara sant kan man i alla fall tycka! Har tentan imorgon så det blir kanske svårt…
Okej. Jag är inte matematiker men för mig är det väldigt uppenbart att gränsvärdet inte existerar då det beror på riktning.
Om detta är slutsatsen under användning av en konvention som säger att tredjeroten ej är definierad för x mindre än noll, så visst. Poängen med den konventionen känns dock meningslös men kanske sparar den tid. Du kan oavsett enkelt lösa uppgiften utan någon sådan konvention. Jag tycker bara den krånglar till det i detta fall.
Det är ur facit till en extenta, så det som står i den borde ju vara sant kan man i alla fall tycka!
Det ska du aldrig anta. Kan alltid stå fel.


