Gränsvärde för talföljd

Hej, jag håller på och övar till en tent men sitter fast. Jag vill visa med hjälp av definitionen gränsvärdet för följande talföljd:

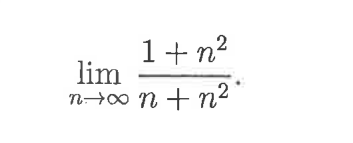
Jag har börjat med att kolla med räknaren gränsvärdet (som är 1) och har skrivit upp enligt definitionen:

$|\frac{1 + n^{2}}{n + n^{2}} - 1| = \frac{1 - n}{n + n^{2}} < ε$

(Skrev inte alla mellansteg hur jag förenklade termerna men ni fattar förhoppningsvis)

Men jag tycker att det är väldigt svårt att nu välja n. Jag vet att n> n_epsilon men har någon ett tips hur man går till väga?

I en liknande uppgift löste jag olikheten så att jag fick att n> 1+ 1/epsilon men denna olikhet jag nu har är rätt så svår.

Du skulle kunna göra så här:

$\frac{1 - n}{n + n^{2}} = \frac{1 - n}{n * (1 + n)} = \frac{1}{n * (1 + n)} - \frac{n}{n * (1 + n)} = \frac{1}{n * (1 + n)} - \frac{1}{1 + n}$

Dessa termer borde båda gå mot noll då n går mot oändligheten.

Jag antar att uppgiften är att visa att för alla värden på epsilon finns ett n-värde sådant att värdet alltid understiger epsilon; det kanske man kan få ut lättare om man gjort ovanstående omskrivning.

Sorry för att bilden är fel svängd. Här är alltså en liknande uppgift som jag fattade.

Om (1 - n)/(n + n^2) < ε, så är

ε(n + n^2) + n > 1. Denna olikhet är satisfierad för t.ex n > 1/ε.

Gustor skrev:
Om (1 - n)/(n + n^2) < ε, så är

ε(n + n^2) + n > 1. Denna olikhet är satisfierad för t.ex n > 1/ε.

Tack ! det var det här jag undrade.

Jag kollade bara på termen εn i VL och såg att resterande termer blev > 0 för n = 1/ε. Kanske hjälper det i framtiden med likande uppgifter.

Svara

Visa senaste svar