Gränsvärde då x går emot oändlighet

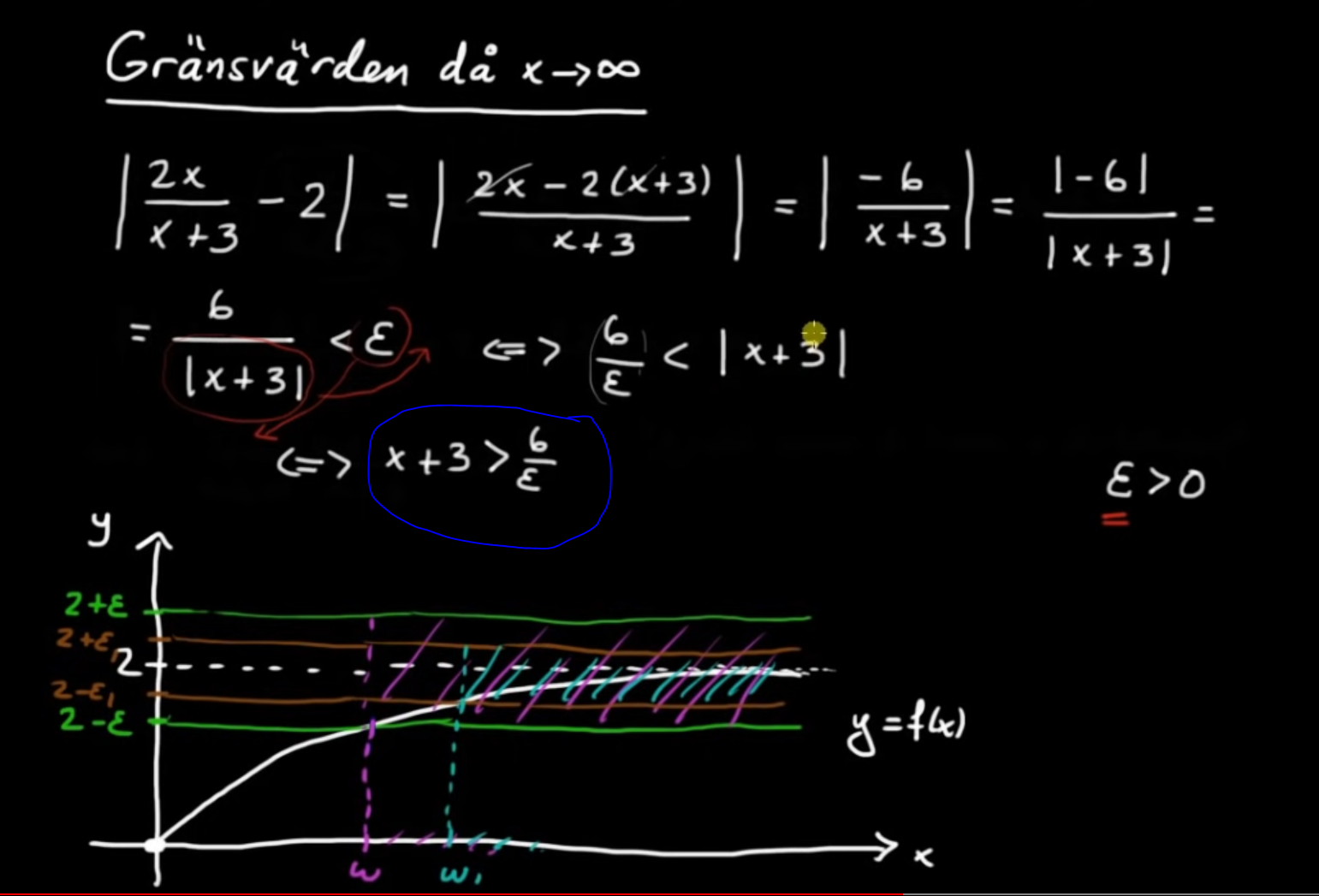
Frågan är lite märkligt formulerad. Det står inte i din bild att x+3>6/epsilon och det är naturligtvis inte heller sant rent generellt. Det som står är att x+3>6/epsilson är ekvivalent med 6/epsilon <|x+3| men inte heller det är generellt sant, det är dock sant för positiva x.

Vi behöver helt enkelt lite mer info om uppgiften för att kunna hjälpa dig.

Nä men om jag ska tolka lite nu, så verkar uppgiften gå ut på att visa:

$\underset{x\to \infty }{\lim }\frac{2x}{x+3}=2$

Då ska vi enligt definition av gränsvärde bevisa att för varje $\epsilon >0$ så existerar ett $\delta$ sådant att $x>\delta \Rightarrow |\frac{2x}{x+3}-2|<\epsilon$.

Det du nu har klistrat in motiverar att

$|\frac{2x}{x+3}-2|<\epsilon \iff x+3>\frac{6}{\epsilon }$

Då är ett outtalat antagande att x>0  men det är ok att anta eftersom vi är intresserade av stora positiva x.

Nu frågar du 

Varför är det så trivial att "x+3>6/epsilon" ??

Men det är lite av ett missförstånd. Påståendet gäller som sagt inte i allmänhet. Däremot gäller det för tillräckligt stora x . Mer precis kan vi sätta

$\delta =\frac{6}{\epsilon }-3$

och då gäller

$x+3>\frac{6}{\epsilon }$

för alla x>$\delta$.

Förstår du nu?