gränsvärde.
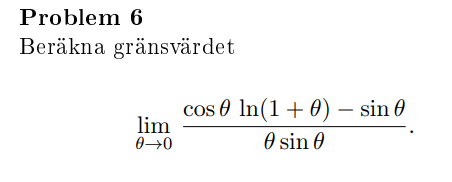
Jag försöker att lösa denna uppgift. jag tänker mig att:
cosx går mot 1
ln(1+x) går mot 0
sinx går mot 0.
x går mot 0
sinx går mot noll.
Så jag tänker mig att jag får 1/nästan0 som då borde gå mot plus oändligheten. Tänker jag rätt?

Hur fick du täljaren att gå mot 1 då båda termerna i täljaren går mot 0? Tänk på att 1 x 0 = 0.
PATENTERAMERA skrev:Hur fick du täljaren att gå mot 1 då båda termerna i täljaren går mot 0? Tänk på att 1 x 0 = 0.
Just, tack!
Då får jag ett gränsvärde [0/0].
Vilken metod bör jag använda för att tackla problemet? Kollar igenom de olika standgränsvärdena mer ingen som jag kan använda där.

Jag skulle använda McLaurin-utveckling.
Laguna skrev:Jag skulle använda McLaurin-utveckling.
Är det bättre att använda McLaurin-utveckling istället för L'Hopitals regel?
Philip22 skrev:Laguna skrev:Jag skulle använda McLaurin-utveckling.
Är det bättre att använda McLaurin-utveckling istället för L'Hopitals regel?

Tror att jag lyckades få rätt genom att ändra runt lite med standardgränsväden. Är det rätt till ? Kan jag komma vidare därifrån?
Jan Ragnar skrev:
Tror att svaret ska bli (-1/2) enligt photomath. Men jag får att detta gränsvärde går mot 0. Misstänker att är fel
Det blir fel för att du räknar en del av gränsvärdet i mitten (blå och röd ring). Det vill man aldrig göra, och uppgifter är ofta riggade för att ge fel svar om man försöker.
Är det tänkt att du ska använda standardgränsvärden? Om det ens går. För det blir mycket enklare med McLaurin.
Micimacko skrev:Det blir fel för att du räknar en del av gränsvärdet i mitten (blå och röd ring). Det vill man aldrig göra, och uppgifter är ofta riggade för att ge fel svar om man försöker.
Är det tänkt att du ska använda standardgränsvärden? Om det ens går. För det blir mycket enklare med McLaurin.
Ok, tack för bra svar! Ska försöka med McLaurin.






