gränsvärde
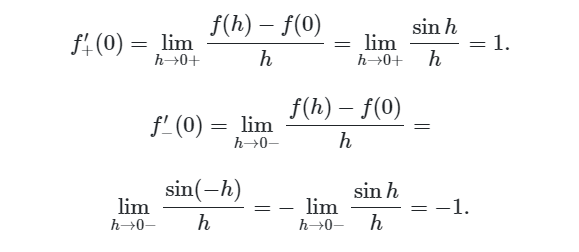
När sinh närmar sig 0+. Alltså h närmas som noll från höger borde det inte bli sin0?
Hur blir det sinh?
sin h går mot 0 när h går mot noll, så täljaren går mot noll.
Kruxet är att även nämnaren går mot noll så vi betraktar ett uttryck på formen 0/0.
Division med noll är inte definierat, så vi kan bara undersöka vart kvoten är på väg när h blir mindre och mindre.
En figur kan hjälpa här. Rita en enhetscirkel, första kvadranten. Markera en vinkel h. Då är h bågens längd i radianer. sin h är längden av linjen som går vinkelrätt mot x-axeln. När h blir allt mindre kommer bågen och linjen nästan smälta samman. Detta är inget bevis, men gör det troligt att gränsvärdet är 1.
Svårt att förklara utan att bli mångordig och utan figur. Men om du har en lärobok finns sannolikt den illustration jag beskriver där.
Marilyn skrev:sin h går mot 0 när h går mot noll, så täljaren går mot noll.
Kruxet är att även nämnaren går mot noll så vi betraktar ett uttryck på formen 0/0.
Division med noll är inte definierat, så vi kan bara undersöka vart kvoten är på väg när h blir mindre och mindre.
En figur kan hjälpa här. Rita en enhetscirkel, första kvadranten. Markera en vinkel h. Då är h bågens längd i radianer. sin h är längden av linjen som går vinkelrätt mot x-axeln. När h blir allt mindre kommer bågen och linjen nästan smälta samman. Detta är inget bevis, men gör det troligt att gränsvärdet är 1.
Svårt att förklara utan att bli mångordig och utan figur. Men om du har en lärobok finns sannolikt den illustration jag beskriver där.
Hej,
tack för svar! Fårstår lite bättre
Kunde hitta i läroboken att gränsvärdet för sinh/h=1 då x går mot noll.
Om jag vet det kan jag utifrån det dra en slutsats att sinh/h=-1 då x går -noll?
Nope, både sin h och h är negativa när h går mot 0– så gränsvärdet är likafullt ett.
Marilyn skrev:Nope, både sin h och h är negativa när h går mot 0– så gränsvärdet är likafullt ett.
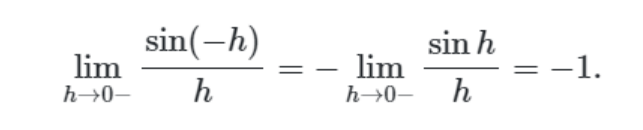
tack, ok! Ser ut som att de bryter ut -1. att det de tar bort minus i sin(-h) och sätter det framför gränsvärdet.
Kan man göra det i alla gränsvärden? Eller bara trigonometriska funktioner?
Du glömde att nämna din ursprungliga funktion. Vad är f(x)?
Ser ut som att de bryter ut -1. att det de tar bort minus i sin(-h) och sätter det framför gränsvärdet.
Kan man göra det i alla gränsvärden? Eller bara trigonometriska funktioner?
Du kan göra det med udda funktioner. T.ex. cos är en jämn trigonometrisk funktion, du får inte göra det med cos. (Det handlar inte om att "bryta ut" -1, -1 är ingen faktor.)
sin (–h) = –sinh men det handlar inte om att bryta ut.
T ex cos(–h) = cos h
Macilaci skrev:Du glömde att nämna din ursprungliga funktion. Vad är f(x)?
Ser ut som att de bryter ut -1. att det de tar bort minus i sin(-h) och sätter det framför gränsvärdet.
Kan man göra det i alla gränsvärden? Eller bara trigonometriska funktioner?
Du kan göra det med udda funktioner. T.ex. cos är en jämn trigonometrisk funktion, du får inte göra det med cos. (Det handlar inte om att "bryta ut" -1, -1 är ingen faktor.)
Ursäkta du hade redan svarat.
Det måste vara vettigt om vi kom på samma tanke samtidigt. :)
Men nu är jag nyfiken: vad är f(x)?
Macilaci skrev:Det måste vara vettigt om vi kom på samma tanke samtidigt. :)
Men nu är jag nyfiken: vad är f(x)?
f(x)=sin|x|
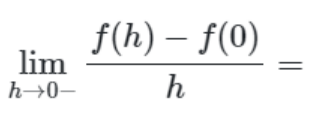
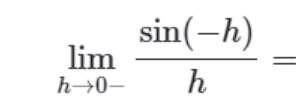
Tror att jag förstår nu varför det blir -h, eftersom h nämar sig noll från vänster och är där med negativt.
Sedan hänger jag med att sinus är ett udda funktion så att sin(-h)=-sin(h)
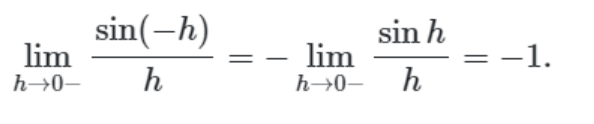
I detta steg ser det ut som att de bryter ut -1, det minustecknet som hamnar framför gränsvärdet. Vad man alltid bryta ut -1 på det sättet? Funkar det för konstanter också?
Men f(x) = sin|x| är inte en udda funktion.
De byter tecken på sin(x) och inte på f(x).
sin(-x) är ju lika med -sin(x)
Jaha, nu ser jag.
Vad man alltid bryta ut -1 på det sättet? Funkar det för konstanter också?
(Som sagt, man bryter inte ut -1.)
Som sagt, det är någonting man kan göra med udda funktioner, men det betyder inte att man alltid bör göra det.
I det här fallet ser man att uttrycket liknar något man känner (nämligen sinx/x) och man försöker göra identiska ändringar för att kunna hamna på
limx→0sin(x)x som är lika med 1.


