Gränsvärde
Hej, jag har svårt med att lösa följande gränsvärde:
https://gyazo.com/2dece46c4dc806e16182a147255d0949
Min tankar: Jag har försökt att göra diverse substitutioner, y = 2x, y = sin(x) och så vidare utan mycket framgång, ofta hamnade jag där jag började. Jag har försökt att utveckla nämnare och dela upp täljaren i delbråk dock kom det heller inte så långt. All hjälp som jag kan få värderar jag otroligt mycket! Behöver gärna vägledning i form a metod eller tips!
Tack på förhand!
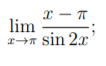
La in din bild. Så här gör man för att lägga in en bild. /Smaragdalena, moderator
.
Prova med ett variabelbyte samt trig. omskrivning.
Jag låter ”standardgränsvärde” slinka över mina läppar ....
Jag skulle först köra på så att du får:
Nu händer något spännande om vi låter . Kan du se vad jag menar?
AlvinB skrev:Jag skulle först köra på så att du får:
Nu händer något spännande om vi låter . Kan du se vad jag menar?
Jag tror det! Du kan hädan efter utveckla sin i nämnare enligt additionsformeln för att få u/sin(u) varefter gränsvärdet går mot 1/2 då u går mot noll? Tack.
Ja. Med får vi:
Detta är ett välkänt standardgränsvärde, och vi får:
En litet tips för att slippa använda additionsformeln är att komma ihåg att perioden för sinusfunktionen är , och alltså blir för alla . Detta ger oss direkt att .



