gränsvärde

Du skulle kunna testa ett variabelbyte h=1/x. Sedan skulle jag l’hopitala här. Varför är det inte aktuellt?

ln(....) fungerar bra. Du får ett gränsvärde =0 vilket ger det sökta gränsvärdet 1

Nayette: Ang. L'Hospital. Enbart (?) tekniska högskolor anv. denna regel. Matematiklinjen gör det ej. Den kanske inte anses "rumsren". På min tid var svaret givet när någon student frågade: "Om du använder LH, var beredd på att bevisa den på muntlig tentamen". Ingen anv. LH... Inte oöverkomlig att bevisa, men "minsta möjliga motståndets lag" gäller... :)

Ja det var det jag tänkte med så jag känner att jag är på god väg med att använda ln, MEN det som stör mig är att jag trots allt får ett "0/0" fall...?

kaffemedmjolk skrev:

Ja det var det jag tänkte med så jag känner att jag är på god väg med att använda ln, MEN det som stör mig är att jag trots allt får ett "0/0" fall...?

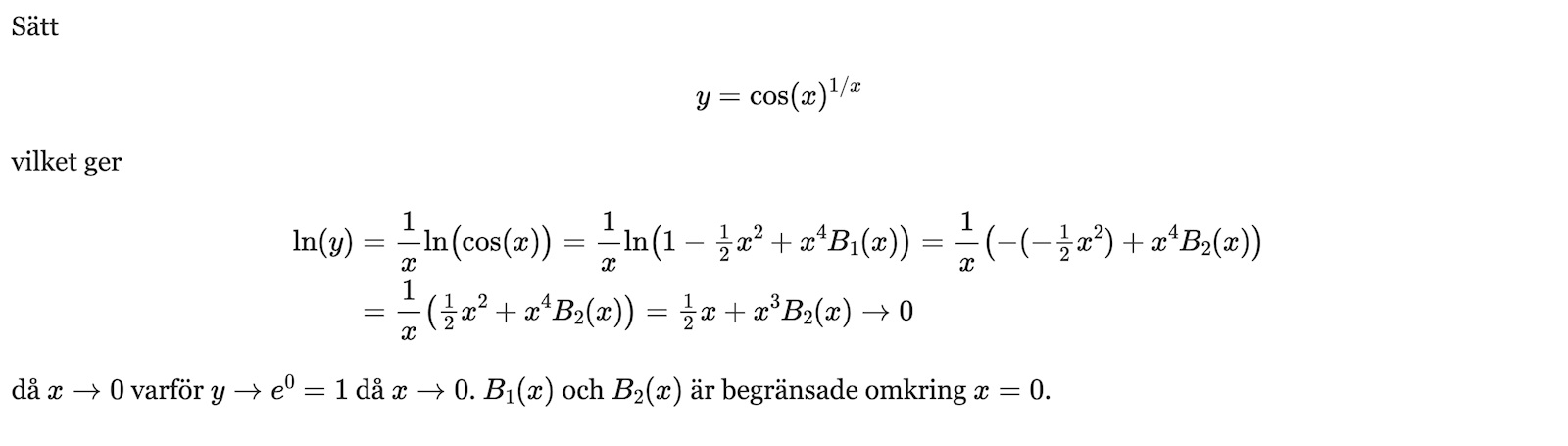
https://mathb.in/80498

Har lite svårt att tolka vad B är för något. Men det är inte behjälpligt oavsett då det känns som en allt för komplicerad lösning för att vara i början av kursen, även om försöket självfallet är tacksamt! Finns det någon annan, mer straight forward, lösning? Går det att resonera fram med hastighetstabell?

$\underset{x\to 0}{\lim }\frac{ln\left(\cos x\right)}{x}$ = $\underset{x\to 0}{\lim }\frac{\ln \left(\cos \left(x\right)\right)-\ln \left(\cos \left(0\right)\right)}{x}={\overline{)\frac{d}{dx}\left(\ln \left(\cos \left(x\right)\right)\right)}}_{x=0}$= -sin(0)/cos(0) = 0.

PATENTERAMERA skrev:

$\underset{x\to 0}{\lim }\frac{ln\left(\cos x\right)}{x}$ = $\underset{x\to 0}{\lim }\frac{\ln \left(\cos \left(x\right)\right)-\ln \left(\cos \left(0\right)\right)}{x}={\overline{)\frac{d}{dx}\left(\ln \left(\cos \left(x\right)\right)\right)}}_{x=0}$= -sin(0)/cos(0) = 0.

Det där är väl L'Hopital. Det är inte aktuellt för just denna uppgift tyvärr :/ 

PANTENTERAMERA använder inte LH utan derivatans definition. Det kan vara en bra metod ibland.

Precis, derivatans definition, inte L’Hospital.