Gränsvärde
Jag har löst den här på följande sätt
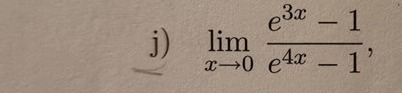

Finns det något enklare sätt? Har använt substitution i andra upg men hittar inte nån här:/
Jag skulle nog använt L'Hôpitals regel, alternativt MacLaurinutvecklingen för eax.
Här en variant på L’Hopital: Sätt f(x)=e3x och g(x)=e4x. Då är (e3x-1)/(e4x-1) = (e3x-1)/x•((e4x-1)/x)-1=
(f(x)-f(0))/x•((g(x)-g(0))/x)-1
–>f’(0)•(g’(0))-1 =
3/4 när x—>0. (Derivatans definition).
Tomten skrev:Här en variant på L’Hopital: Sätt f(x)=e3x och g(x)=e4x. Då är (e3x-1)/(e4x-1) = (e3x-1)/x•((e4x-1)/x)-1=
(f(x)-f(0))/x•((g(x)-g(0))/x)-1–>f’(0)•(g’(0))-1 =
3/4 när x—>0. (Derivatans definition).
Lhopital kommer lite senare fram, finns det något ytterligare sätt att lösa denna?
Förslaget ovan vilar inte på L’Hopital utan på derivatans definition. Men på detta sätt kan L’Hopital bevisas i detta fall.
Tomten skrev:Förslaget ovan vilar inte på L’Hopital utan på derivatans definition. Men på detta sätt kan L’Hopital bevisas i detta fall.
Aha okej tack
Du kan använda infinitesimaler, vilket jag hintade lite åt i en av dina andra trådar. Vi kan tänka oss följande:
limx→c(f)=std(f(c)), där std betecknar standarddelen av f(c).
I ditt fall kan vi göra så här:
limx→0e3x-1e4x-1=limx→0+e3x-1e4x-1=std(eε)3-1(eε)4-1=...
där ε är en positiv infinitesimal. Om man slutför detta resonemang kommer man också fram till 3/4.
Det var ungefär på detta sätt matematiker på 1700- och 1800-talet löste "gränsvärden" (gränsvärden var inte riktigt formaliserade på den tiden).
Tveksamt dock om detta ger poäng på en tenta i reell analys :)
Tillägg: 10 aug 2024 16:37
Vet heller inte om det är så mycket enklare än det du gjorde. Kanske lite mer intuitivt...?
naytte skrev:Du kan använda infinitesimaler, vilket jag hintade lite åt i en av dina andra trådar. Vi kan tänka oss följande:
limx→c(f)=std(f(c)), där std betecknar standarddelen av f(c).
I ditt fall kan vi göra så här:
limx→0e3x-1e4x-1=limx→0+e3x-1e4x-1=std(eε)3-1(eε)4-1=...
där ε är en positiv infinitesimal. Om man slutför detta resonemang kommer man också fram till 3/4.
Det var ungefär på detta sätt matematiker på 1700- och 1800-talet löste "gränsvärden" (gränsvärden var inte riktigt formaliserade på den tiden).
Tveksamt dock om detta ger poäng på en tenta i reell analys :)
Tillägg: 10 aug 2024 16:37
Vet heller inte om det är så mycket enklare än det du gjorde. Kanske lite mer intuitivt...?
Hihi men tack ändå, detta är envariabel😭
Fördelen med sådana "metoder" är att de ger en mycket mer intuitiv överblick av vad som händer. I många fall kan man också lösa gränsvärdet ganska fort och att veta vad svaret ska bli kan ju aldrig skada... :)
naytte skrev:Fördelen med sådana "metoder" är att de ger en mycket mer intuitiv överblick av vad som händer. I många fall kan man också lösa gränsvärdet ganska fort och att veta vad svaret ska bli kan ju aldrig skada... :)
True tho, ska försöka bli bättre på att använda de🥹
Man kan använda serieutvecklingen:
eax=1+ax+O(x2)
limx→0e3x-1e4x-1=
limx→01+3x-11+4x-1=
limx→03x4x=34
tomast80 skrev:Man kan använda serieutvecklingen:
eax=1+ax+O(x2)
limx→0e3x-1e4x-1=
limx→01+3x-11+4x-1=
limx→03x4x=34
Har aldrig sett den innan, men tack👀
Det är Taylorutvecklingen av funktionen.



