Gränsvärde
Jag ska lösa
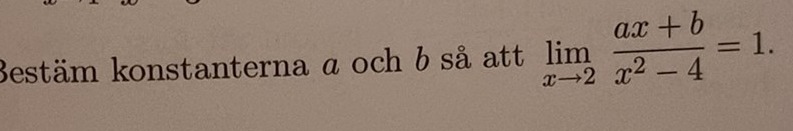
När man gick igenom detta så sa läraren att "Eftersom nämnaren går mot 0 så går också nämnaren mot 0", men jag har löst andra uppgifter med gränsvärde där täljaren och nämnaren inte båda går åt samma sak?
Eller jag förstår det nu, men undrar dock: när jag fortsätter så sätter jag då 2a+b=0
Men när jag sätter in b i formeln så har han inte med x. Varför är det så?
Vad menar du? Ur ditt samband kan du lösa fram . Du får då:
Faktorisera nämnaren och bestäm !
Löste det sig då? :)
naytte skrev:Vad menar du? Ur ditt samband kan du lösa fram . Du får då:
Faktorisera nämnaren och bestäm !
Löste det sig då? :)
Visa spoiler
Skriv ditt dolda innehåll här
Är det för att jag har x upphöjt i något och måste faktorisrta först innan jag sätter in x=2?
Du "måste" ingenting. Men du vill ju "dela bort" den del av funktionen som blir noll i nämnaren. Den faktorn råkar vara i nämnaren. Kan du bestämma så att du kan dela med i både nämnare och täljare?
naytte skrev:Du "måste" ingenting. Men du vill ju "dela bort" den del av funktionen som blir noll i nämnaren. Den faktorn råkar vara i nämnaren. Kan du bestämma så att du kan dela med i både nämnare och täljare?
Jag fattar den delen att jag kan göra så, men naturligt så vill jag stoppa in x också och lösa ut a, men det blir fel då:/

Du måste fiffla lite med uttrycket innan du kan byta ut mot , annars delar du ju med och det är odefinierat! Jag menar att du ska göra så här:
Tar du det därifrån? :)
naytte skrev:Du måste fiffla lite med uttrycket innan du kan byta ut mot , annars delar du ju med och det är odefinierat! Jag menar att du ska göra så här:
Tar du det därifrån? :)
Ohhh right, tack så mycket😭


