gradient

Den lättaste förklaringen jag hittat av gradienter: 

Tänk dig ett plan, ett helt vanligt xy-plan, som lutar åt något håll. På planet ligger en rund boll. Den kommer att rulla i den riktning som planet lutar:

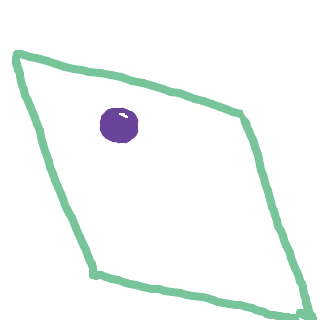
Om vi vill hitta denna lutning, kan vi undersöka hur planet lutar i x-led, samt i y-led. Detta gör vi genom att hitta den partiella derivatan med avseende på x respektive y. Om vi nu tänker oss att bollen ska rulla en liten bit, kan vi tänka oss att bollen först rullar längs lutningen med avseende på x-axeln, och sedan rullar längs lutningen med avseende på y-axeln:

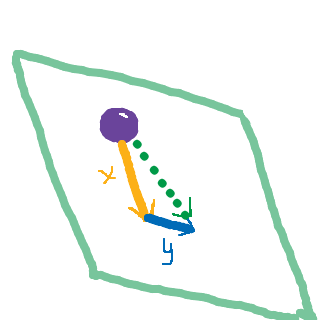
Den gröna, resulterande rörelsen är den brantaste lutningen längs planet. Den får vi genom att rulla längs den sträcka i x- respektive y-led där det lutar som mest. Denna resulterande lutning är alltså där bollen skulle accelerera fortast om den rullade. Den pilen (vektorn) är den maximala lutningen, och vektorn som går i motsatt riktning (dvs. maximal uppförsbacke) är gradienten. :)

EDIT: Kommentar om gradientens riktning tillagd. Tack Qetsiyah! :)

Hej,

• I en dimension kan man bara röra sig i en riktning: framåt eller bakåt. För att se hur en funktions värde f(x) förändras då x ändras används funktionens derivata $f^{\prime}.$
• I två dimensioner kan man röra sig i  flera riktningar; samtliga riktningar kan uttryckas med rörelse i x-led och rörelse i y-led. Man skriver detta som en linjärkombination $v = xe_x+ye_y$ av riktningarna $e_x=(1,0)$ och $e_y=(0,1).$ För att se hur en funktions värde $f(x,y)$ förändras då $(x,y)$ ändras i riktningen $v$ används de partiella derivatorna $\frac{\partial f}{\partial x}$ och $\frac{\partial f}{\partial y}$ så att den sökta förändringen är linjärkombinationen $v \cdot \nabla f(x,y)$.

Smutstvätt skrev:

Den lättaste förklaringen jag hittat av gradienter: 

Tänk dig ett plan, ett helt vanligt xy-plan, som lutar åt något håll. På planet ligger en rund boll. Den kommer att rulla i den riktning som planet lutar:

Om vi vill hitta denna lutning, kan vi undersöka hur planet lutar i x-led, samt i y-led. Detta gör vi genom att hitta den partiella derivatan med avseende på x respektive y. Om vi nu tänker oss att bollen ska rulla en liten bit, kan vi tänka oss att bollen först rullar längs lutningen med avseende på x-axeln, och sedan rullar längs lutningen med avseende på y-axeln:

Den gröna, resulterande rörelsen är den brantaste lutningen längs planet. Den får vi genom att rulla längs den sträcka i x- respektive y-led där det lutar som mest. Denna resulterande lutning är alltså där bollen skulle accelerera fortast om den rullade. Den pilen (vektorn) är gradienten. :)

Jag hade länge problem med att visualisera sådant här, kanske för att "man" också hör att gradienten är normal till en yta.

Om man har funktionen f(x,y) så kan vi plotta/visualisera den som z=f(x,y) vilket skapar ett "landskap" i R3. Det jag länge såg framför mig var att om gradienten pekar i den riktning som f ökar som mest borde gradienten vara en vektor parallell med ytan som pekade åt den riktning där landskapet gick så mycket som möjligt "uppåt", dvs om jag följer längs med gradienten skulle jag klättra upp för en backe. Det sade helt emot det jag hört att gradienten också är normal till en yta (i resonemanget tidigare var den ju en tangent). Men gradienten av f(x,y) kommer ju vara en 2-dimensionell vektor så det är ju omöjligt att gradienten så att säga pekar mot en punkt högre upp i landskapet (eftersom gradienten är 2D och landskapet är 3D). Det jag efter lite tanke kom fram till är en lämplig visualisering för mig är att jag ska se mig själv som att man står på xy-planet och att nivåytan z=f(x,y) är ett tak. Gradientens riktning (som är längs xy-planet) är då den riktning jag ska gå längs med xy-planet om jag vill att taket ska höjas så snabbt som möjligt. 

Att då säga att en boll kommer rulla åt ett visst håll känns för mig svårt att ta in eftersom det snarare leder mig in på tanken att gradienten pekar längs nivåytan z=f(x,y)

Det här med att gradienten är normalen blir då för mig också enklare att förstå. Gradienten av f(x,y) blir ju normalen till nivåkurvorna f(x,y)=C. Om jag tar exempelvis $f(x,y)=x^2+y^2$ och ritar nivåkurvor blir det cirklar i xy-planet. Normalen till dessa cirklar pekar rakt bort från origo. Om jag sedan visualiserar funktionen som z=f(x,y) ser jag att funktionsvärdet (dvs z-koordinaten) ökar som mest för det punkterna i xy som ligger rakt bort från origo. Gradienten är då normal (till nivåkurvorna i xy-planet) och samtidigt den riktning jag ska gå för att få funktionsvärdet f(x,y) att öka så snabbt som möjligt. Och jag har då en mindre grej att grubbla på.... :)

Om du stirrar länge nog på den här vackra bilden kommer du förstå (det funkade för mig, jag älskade den här bilden):

Smutstvätt: den gröna vektorn i din bild är väl inte gradienten? Det är minus den vektorn. Det är inte heller så bra att visualisera sådär, gradienten är en vektor i R2 (inte R3) trots att grafen {(x, y, z): z=f(x,y)} är i R3.

@Qetisyah: Hmm, ja jo jag har markerat fel vektor. Jag har lagt till en kommentar om detta. :)

Haha, vad lyxigt att vara moderator

$😉$

Skämt åsido, lite lyxigt är det. :)