givet att minst en av komponenterna fungerar, vad är sannolikheten att a inte fungerar?
Hej! Jag försökte lösa dessa frågor och fick rätt på a)-uppgiften men fel på b). Vet inte riktigt vart det blir fel? facit ger tyvärr bara svaret här och inget lösningsförslag:(.
Jag tänkte att
eftersom att jag C = händelsen att minst en av de fungerar och eftersom att denna ska instämma samtidigt som komponent a inte ska fungera så måste det vara b som fungerar.


tack på förhand!
Din likhet du ställer upp stämmer tyvärr inte. T.ex kommer händelse B även inkludera fallet då A fungerar, eftersom att A och B är oberoende. Likheten du skriver säger att B bara får fungera om A inte fungerar.
Calle_K skrev:Din likhet du ställer upp stämmer tyvärr inte. T.ex kommer händelse B även inkludera fallet då A fungerar, eftersom att A och B är oberoende. Likheten du skriver säger att B bara får fungera om A inte fungerar.
Ah okej! kan man tänka istället att ?
Nej, däremot kan du säga att P(Ac snitt C) = P(Ac union C) - P(Ac\C) - P(C\Ac), men jag har svårt att se att det leder till framåt i lösningen.
Med ett fåtal utfall (2 x 2) så blir det ofta väldigt smidigt om man ritar ett träddiagram.
Calle_K skrev:Nej, däremot kan du säga att P(Ac snitt C) = P(Ac union C) - P(Ac\C) - P(C\Ac), men jag har svårt att se att det leder till framåt i lösningen.
Ah okej:(
Dr. G skrev:Med ett fåtal utfall (2 x 2) så blir det ofta väldigt smidigt om man ritar ett träddiagram.
Träddiagram?
Utan att ha räknat själv känns det som att Bayes sats skulle kunna hjälpa här
Hejhej! skrev:Dr. G skrev:Med ett fåtal utfall (2 x 2) så blir det ofta väldigt smidigt om man ritar ett träddiagram.
Träddiagram?
Smaragdalena skrev:Hejhej! skrev:Dr. G skrev:Med ett fåtal utfall (2 x 2) så blir det ofta väldigt smidigt om man ritar ett träddiagram.
Träddiagram?
Slog upp det i boken och blev nu påmind men vet inte hur jag ska göra det i detta fall? ska jag göra ett träddiagram mellan A och C eller A och B?
Slog upp det i boken och blev nu påmind men vet inte hur jag ska göra det i detta fall? ska jag göra ett träddiagram mellan A och C eller A och B?
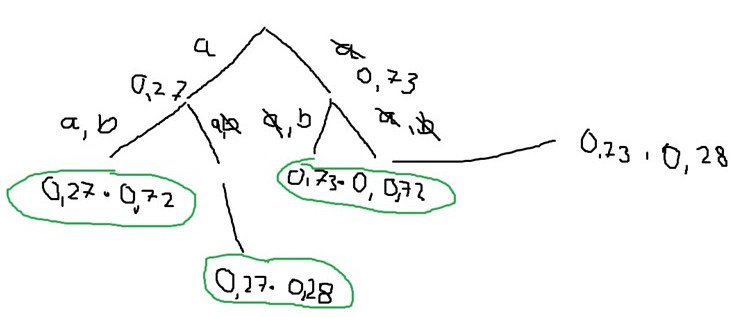
Situation c är det som jag har ringat in med grönt. Kommer du vidare härifrån?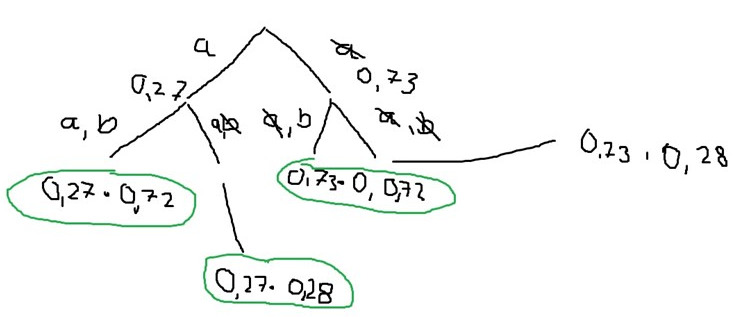
Smaragdalena skrev:Slog upp det i boken och blev nu påmind men vet inte hur jag ska göra det i detta fall? ska jag göra ett träddiagram mellan A och C eller A och B?
Situation c är det som jag har ringat in med grönt. Kommer du vidare härifrån?
Ja nu fick jag rätt svar tack!
När det gäller bara två händelser, a och b, så kan det fungera bra med en 2x2-tabell. I synnerhet om händelserna är oberoende, då kan man skriva in alla sannolikheter direkt.
Laguna skrev:När det gäller bara två händelser, a och b, så kan det fungera bra med en 2x2-tabell. I synnerhet om händelserna är oberoende, då kan man skriva in alla sannolikheter direkt.
ah okej tack!