Gitter och avståndet att beräkna x
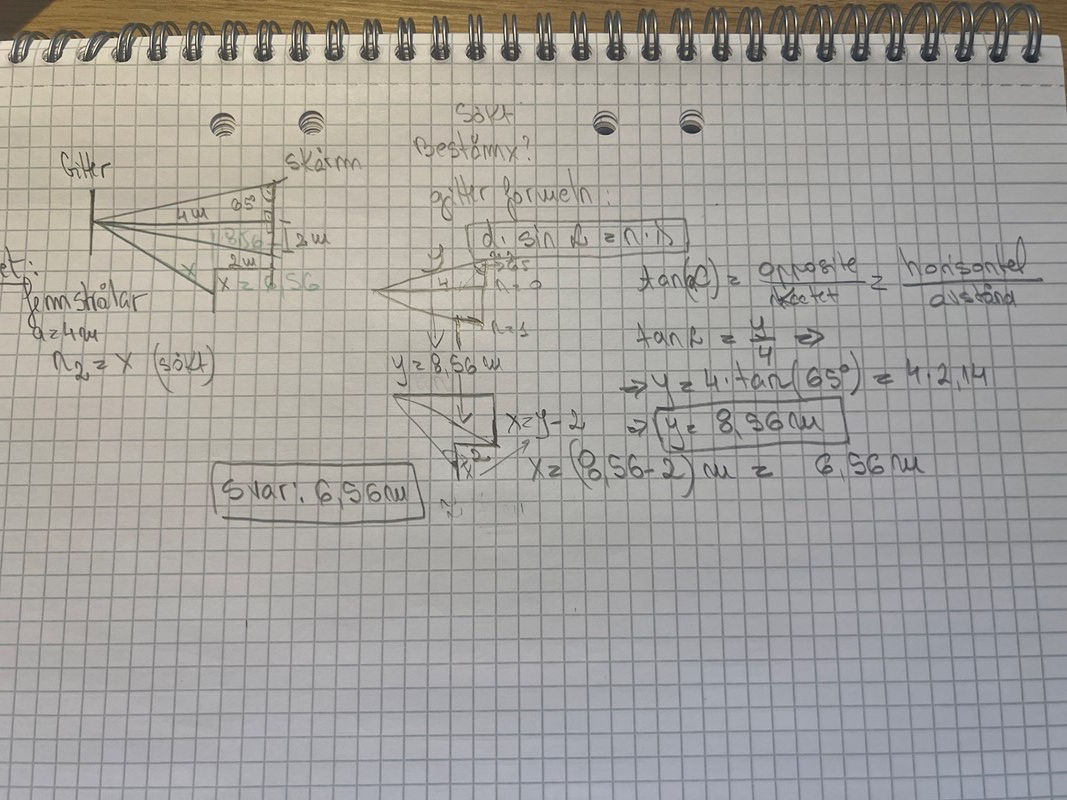
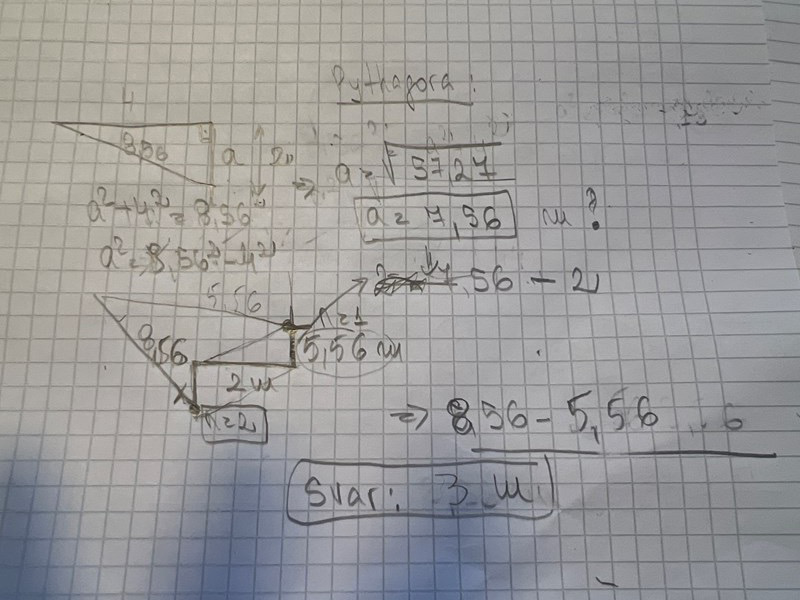
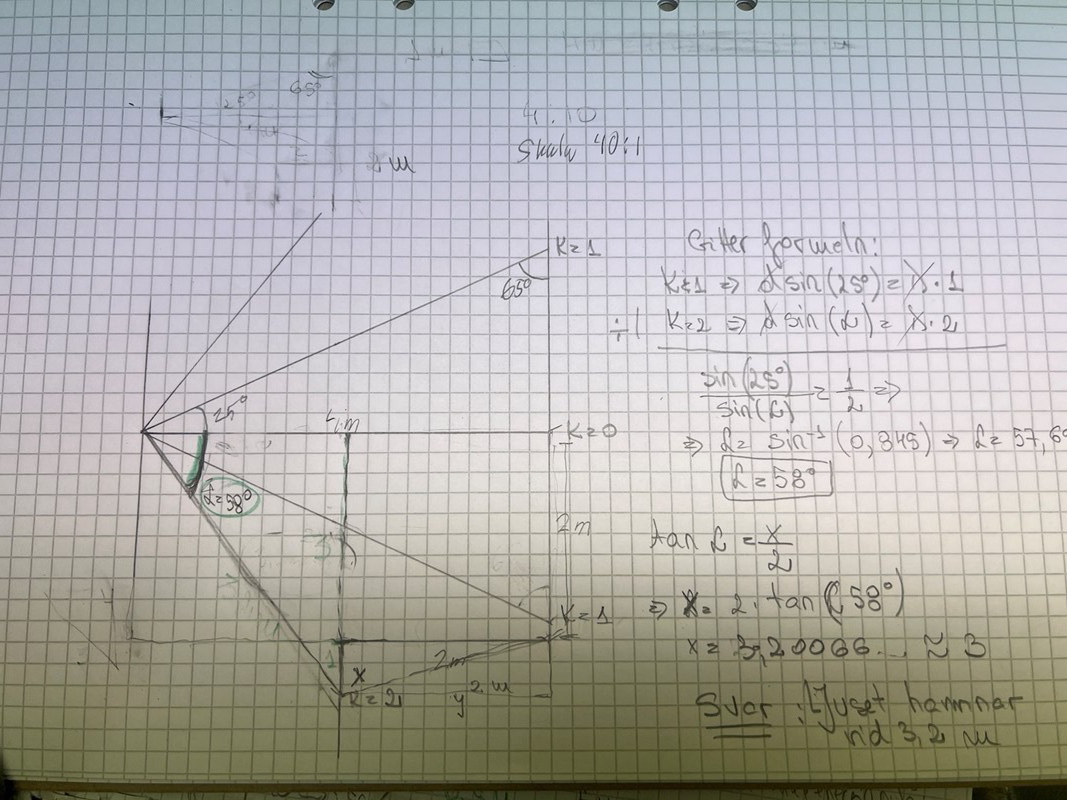
En ljusstråle av viss våglängd passerar genom ett gitter. Fem strålar är utritade och visar var nollte, första och andra ordningens ljusmaxima kommer hamna. Avståndet mellan skärmen och gittret är 4 meter. Andra ordningens ljusmaxima åt höger från gittret sett hamnar på en vägg istället. Bestäm hur långt ifrån hörnet som ljusmaximat hamnar, alltså bestäm x.
jag fårstår inte varför de ger oss 5 stålar,bara att förvirra ?
Cristina skrev:jag fårstår inte varför de ger oss 5 stålar,bara att förvirra ?
De ritade nollte, första och andra ordningen. Det hade kanske inte behövts, jag skulle ha låtit eleverna rita dessa strålar själv om jag hade konstruerat problemet.
Jag förstår inte riktikt vad du gör i din lösning. Kanske är det en genväg som är rätt, men då skulle du behöva argumentera för det. Men tydligare är det att explicit räkna ut vinkeln för diffraktion i andra ordning som ett mellansteg.
hur att argumentera för det? att ritta igen? jag räknar y in första ornding frön symetrilinen med tangent och subtraherar med 2m givet!tack
Cristina skrev:jag räknar y in första ornding frön symetrilinen med tangent och subtraherar med 2m givet!tack
Första ordningen ligger mindre än två meter från symmetrilinjen.
Jag förstår inte.
Enklaste metoden är att först bestämma den här vinkeln: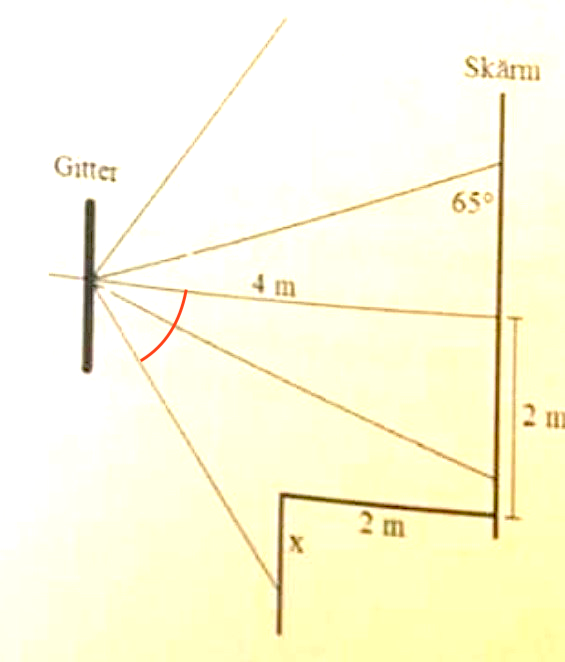
Om du gör en skalenlig ritning ser du att det inte är rätt svar.
Cristina skrev:Bestäm hur långt ifrån hörnet som ljusmaximat hamnar
Läs igen exakt vad uppgiften är och jämför med ditt svar.
??? Jag vet inte hur annars? Var tanker jag fel? 
chat gpt suggest:.Kanshe nu förstår jag!
- Placering på Vägg: När det andra ordningens maxima (m=2) hamnar på väggen, innebär det att vinkeln θ2θ2 för detta maximum är större än 45 grader. Detta resulterar i att maximalens position y2y2 inte längre kan placeras på skärmen utan träffar istället väggen.
-
- Om vi antar att θ2=45∘θ2=45∘ (det minsta möjliga värdet där maxima börjar träffa väggen), blir:x=4×tan(45∘)=4×1=4 meterx=4×tan(45∘)=4×1=4 meter
- Om θ2>45∘θ2>45∘, kommer tan(θ2)>1tan(θ2)>1, vilket innebär att x>4x>4 meter. Eftersom frågan specifikt frågar efter hur långt ifrån hörnet maxima hamnar när de landar på väggen, och med minimal antagning av θ2=45∘θ2=45∘, är den lägsta möjliga värdet för xx 4 meter.
Slutsats: Avståndet xx från hörnet där det andra ordningens ljusmaxima hamnar på väggen är 4 meter.
Svar:Maximatet landar 4 meter från hörnet.
Nej, titta i den ritning som du gjorde. En till mening med att göra en noggrann ritning är att man kan jämföra det uträknade svaret med måtten i figuren. Och då är avståndet till hörnet inte 3,2 meter.
Och ChatGPT är fortfarande värdelöst på sådant.
tack,jag ser inte hur! Hjelp! 4-3,2=0.8 Är det rimligt?
Cristina skrev:tack,jag ser inte hur! Hjelp! 4-3,2=0.8 Är det rimligt?
Negativt? Åt andra sidan??
Det du verkar ha räknat ut som 3,2 meter är den röda linjen nedan. Det är inte vad uppgiften frågar efter.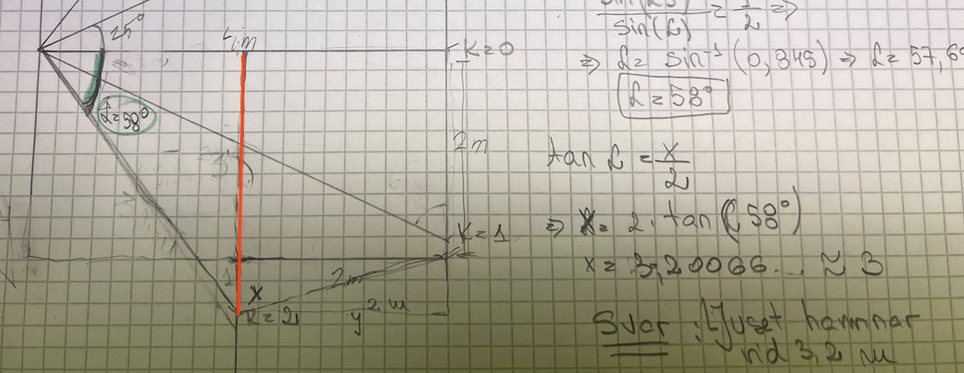
3,2-2= 1,2
Pieter tack för tålamåd
