Gevär
Hur har de fått att sy är 6378 km och att sx är 200+6378 km? Höjden 200 km är ju sy

Lösningen är helt fel. Den räknas med kaströrelse vilket du i detta fall inte får göra.
Jag har en teori om hur de har tänkt fel, men jag vågar inte ens skriva ner den.
Ta bara resultatet: för att kanonkulan bara ska följa jordens yta behöver den flyga med den första kosmiska hastigheten (där centripetalaccelerationen är lika med g) som är 7,9 km/s.
varför får man inte lösa med kaströrelse
Kaströrelse förutsätter ett homogent gravitationsfält. I så fall är banan en parabel. Men i den här uppgiften är banan en ellips.
Men vi säger nu att vi kan lösa denna med kaströrelse, varför blir sy och sx som de blir?
Jag säger inte det. De som skrivit boken blandar (kanske) kaströrelse och planetrörelse. De visste att toppen (apogeum) nås efter en fjärdedel av omloppsbanan. Sedan ritade de den här skissen:
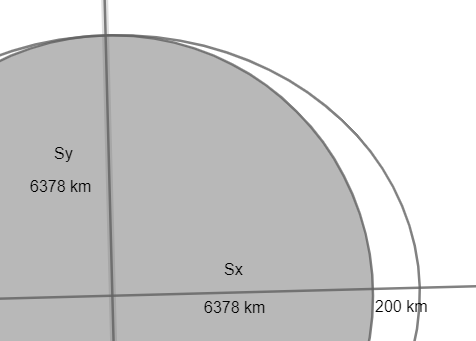
Och började beräkna begynnelsehastigheten av en kaströrelse. Du ser var Sy och Sx kommer ifrån.
Men det skulle innebära att gravitationen pekar nedåt i hela skissen (och banan är parabel och inte ellips).
ahaaa nu förstår jag, det var exakt det jag tänkte, men hur löser jag den annars
Jag skulle säga att det är ett svårt problem. Mitt försök var:
1) Jag beräknade g på 200 km höjd, vilket är 9,23
2) Jag beräknade skillnaden i potensiell energi mellan 0 och 200 km (med hjälp av olika g värden och okänd massa som parameter).
3) Jag antog att den centripetala accelerationen på 200 km höjd är lika med g200km.
4) Jag beräknade hastigheten på 200km
5) Jag antog att minskningen av den kinetiska energin är lika med skillnaden i potensiell energi.
6) Jag beräknade begynnelsehastigheten.
Sen kollade jag mitt resultat med orbit kalkylatorn, och märkte att jag gjorde något fel.
Problemet var att krökningen av den elliptiska banan är lite högre än krökningen av den cirkulära banan Men då släppte jag uppgiften.
okej tack

