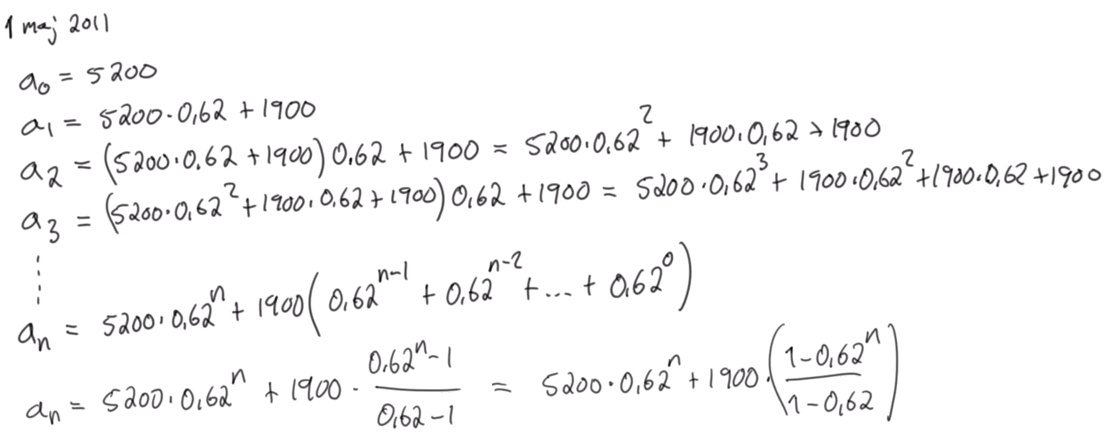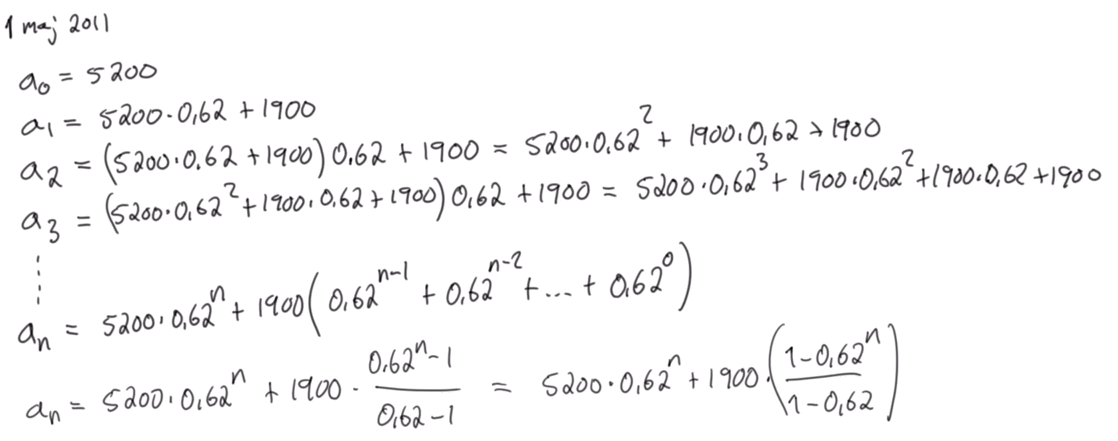Geometrisk summa uttryckt i diffekv?

Jag undrar varför det inte går att lösa uppgifter genom att teckna en differentialekvation och sedan lösa den, där slutligen själva funktion y blir ett uttryck för en sluten formel för an
Förändringhastigeten
vart tänker jag fel?
Lösningen för den som undrar (ej mina beräkningar):
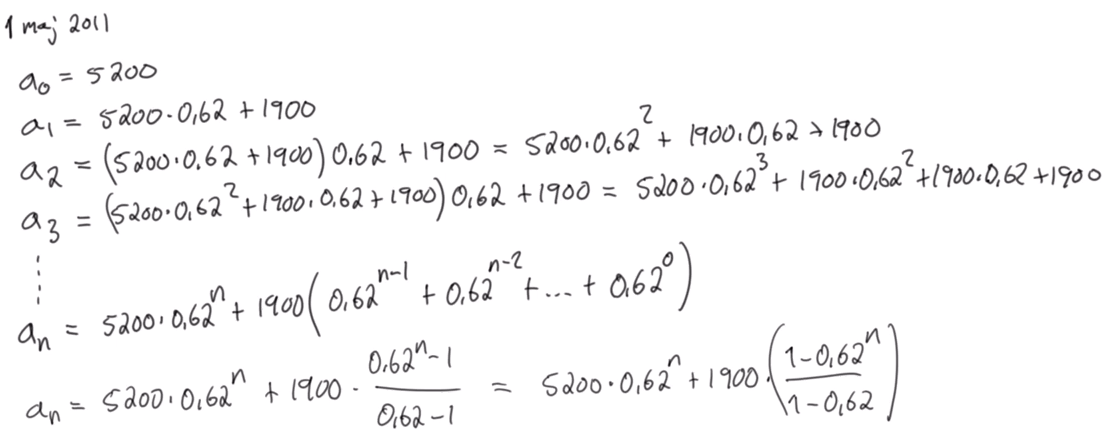
lvl99cooking skrev:
Jag undrar varför det inte går att lösa uppgifter genom att teckna en differentialekvation och sedan lösa den, där slutligen själva funktion y blir ett uttryck för en sluten formel för
vart tänker jag fel?
Lösningen för den som undrar (ej mina beräkningar):
Rita upp de båda funktionerna och jämför. Det kan hända att ditt sätt också funkar. Lägg upp sin bild här om du vill diskutera mer.
Smaragdalena skrev:lvl99cooking skrev:
Jag undrar varför det inte går att lösa uppgifter genom att teckna en differentialekvation och sedan lösa den, där slutligen själva funktion y blir ett uttryck för en sluten formel för
vart tänker jag fel?
Lösningen för den som undrar (ej mina beräkningar):
Rita upp de båda funktionerna och jämför. Det kan hända att ditt sätt också funkar. Lägg upp sin bild här om du vill diskutera mer.

Dom ligger ju relativt nära varandra, men jag tänker ju att det inte sker några avrundningar i någon av beräkningarna så hur kommer det sig att funktionerna skiljer sig? Eller snarare, varför något av räknesätten är fel.
Jag tror att grundproblemet är att du försöker modellera ett diskret förlopp (an räknas årligen) med en differentialekvation innehållandes en kontinuerlig funktion y(t).
Som jag har förstått det så ska diskreta förlopp modelleras med rekursion, eller, som här, på en sluten form.
Okej, jag fattar inte varför svaren skiljer sig åt för heltalvärdens, sätter jag exempelvis in f(3) och g(3) så skiljer sig svaren. Jag kan dock förstå att talföljdens modell är mer rimligt för redovisningsyfte.
I min, något begränsade, matematiska värld så förstår jag inte varför modellernas svar skiljer sig åt när deras uttryck grundar sig på samma information.
I din formel tillsätter man inte alla fiskarna samma dag, utan kontinuerligt, ungefär 5 fiskar per dag. Det borde kunna förklara skillnaderna.
Smaragdalena skrev:I din formel tillsätter man inte alla fiskarna samma dag, utan kontinuerligt, ungefär 5 fiskar per dag. Det borde kunna förklara skillnaderna.
Ja, detta tillsammans med att ett kontinuerligt.bortfall på 38 % inte innebär samma sak som ett sammanräknat årligt bortfall på 38 % gör att resultatet skiljer sig åt.