Geometrisk summa
Har följande formel för en geometrisk summa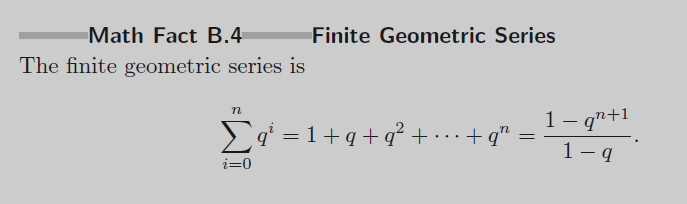
Om jag istället har , där jag vill göra om den till formeln ovan så jag kan utnyttja kvoten. Om jag bryter ut q så får jag nu har jag ordnat så att första termen har i=0 men nu blir sista n-1 istället. Jag skriver om den så här , dvs summan går upp till qn (men detta mutipliceras med en faktor q!!) vilket vi behöver subtrahera bort. Om vi nu sätter ihop allt, stämmer följande?
Det verkar stämma om jag kör det i matlab för något q och något n.
Summan med i = 1 är alltid samma som summan från i = 0 fast utan den första termen, vilket är 1. Därför tänker jag såhär:
Alltså samma svar. Wolfram alpha förenklar också till exakt samma uttryck (förutom att den har bytt plats på minustecknet i täljaren och nämnaren)
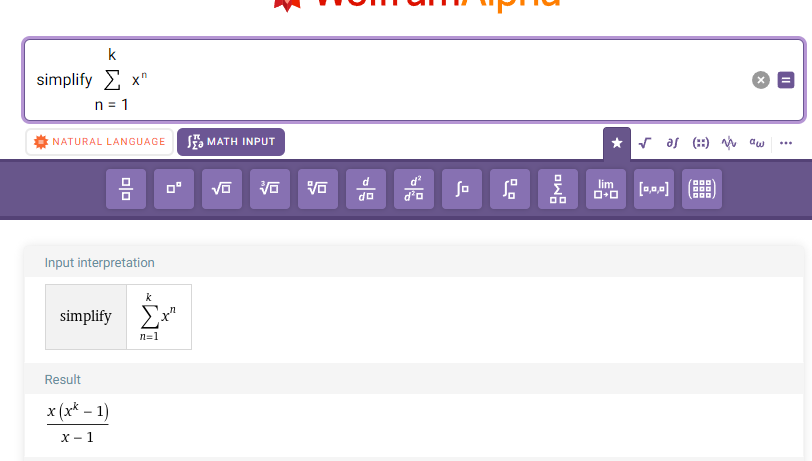
Skillnaden mellan att start med i = 0 och i=1 är bara den första terman '1' så dra bort den ur högerledet så får du efter lite omstuvningar ditt svar så det är korrekt
Edit: 2själar samma tanke - bortde dock ha sett att du skrev....
tack ska ni ha

