Geometri problemlösning
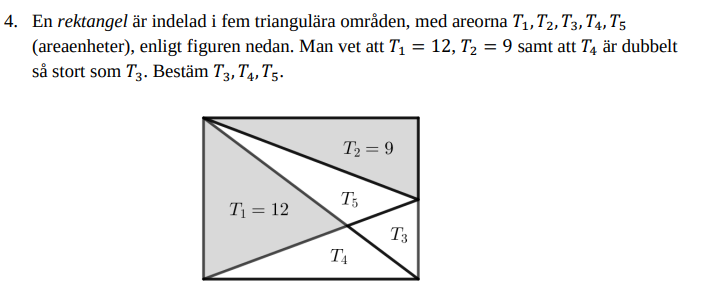
Hej!
Jag har suttit med denna uppgiften länge, men inte lyckats lösa den.
Jag har hittat förhållanden mellan areorna T1 och T2 (4:3), samt förhållanden mellan T3, T4 och T5. (T4=2T3 och T5=T3+3). Jag har därför försökt hitta arean T3 och då kommit fram till att T3 och T1 är likformiga, men det har inte hjälpt. Jag har också kommit fram till att om man kan visa att T1+T5 bildar en likbent triangel eller att T4+T3 bildar en likadan triangel som T2 kan man hitta arean på T3 och därmed lösa uppgiften, men jag har inte lyckats bevisa det. Om annars bevisar att T2 och T3 har lika lång bas så kommer man fram till samma svar. Så jag undrar hur man kan visa något av detta, eller om det finns en enklare lösning på uppgiften.
Tack på förhand!
Välkommen hit, Ellabellabing0!
Ser du att
triangeln som består av. [T5 + T3]
har samma bas och höjd som
triangeln som består av. [T4 + T3].
De har därför samma area.
Kommer du vidare från det?
Tack så jättemycket!
Jag lyckades lösa ut arean T3 som blev 3a.e., vilket stämmer i facit!
Så bra!
Mitt förslag räcker bara till att ge samband mellan T3, T4 och T5.
För att lösa uppgiften måste man också hitta ett samband
mellan en av dessa och någon av de kända trianglarna.
Sedan såg jag att rektangeln innehåller en utritad diagonal.
Den delar rektangeln i två lika stora delar!
Här får vi ett samband till, och det innehåller både T1 och 'T2.
Precis!
Det var med hjälp av det sambandet jag lyckades lösa areorna för T4 och T5 också.
Tack så jättemycket för hjälpen!

