Geometri och Likformighet: Cirklar inskrivna i en triangel
Hej, hur löser man denna uppgiften från PQ 2024?
Har försökt mig på att dra diverse linjer mellan den rosa och vita cirkeln för att försöka hitta något samband mellan dem genom att använda pythagoras sats. Samt att försöka lösa förhållandet mellan rosa och grön med hjälp av vetskapen om att trianglarna som de är inskrivna i är likformiga. Men detta leder inte riktigt någonstans.
Hittills så har jag kommit fram till att trianglarna troligtvis måste vara 30-60-90 trianglar, men hur jag kom fram till det är ytterst oklart.
Uppgiften är tagen från pythagorasquest.se distriktsfinal 2024.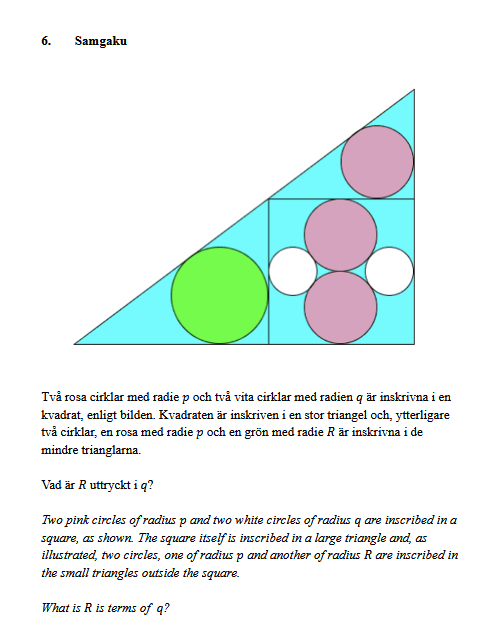
Om vi kallar kvadratens sida 1 så är de rosa cirklarnas radie 1/4. Då vet vi var medelpunkten för cirkeln uppe till höger är.
Tackar, kunde lösa uppgiften med denna information. Eftersom att man nu kan veta att höjden på den vänstra triangeln är 3p ( Kan eventuellt vara så att detta inte stämmer ???). Då får man att relationen mellan R och p är 4:3 . Därefter så kan man skriva kvadratens sida som 3q + 2p, och sedan lösa ut r genom att ställa upp ekvationen 3q +2p = 4p. Och därefter får man att 3/2q = p. Sedan R =(3/2 * 4/3)q = 2q.
Om du ser det här: Menar du 3R i andra meningen? Hur fick du det? Jag är också nyfiken hur fick du kvadratens sida till 3q+2p, alltså att det får plats 3 vita cirklar i bredd i kvadraten?


