Genom att derivera ska man hitta konstanten b

1^1/3=1 och det gäller inte att 3*1^1/3=3^1/3. Du kommer med andra ord få 

a^1/3/3=1/b 

Härifrån kan du lösa den.😃

Men jag får dock fortfarande inte rätta svaret, jag får b=3/a^1/3 men svaret ska vara b=27/a.

Squarerootofconfused skrev:

Men jag får dock fortfarande inte rätta svaret, jag får b=3/a^1/3 men svaret ska vara b=27/a.

https://mathb.in/80874

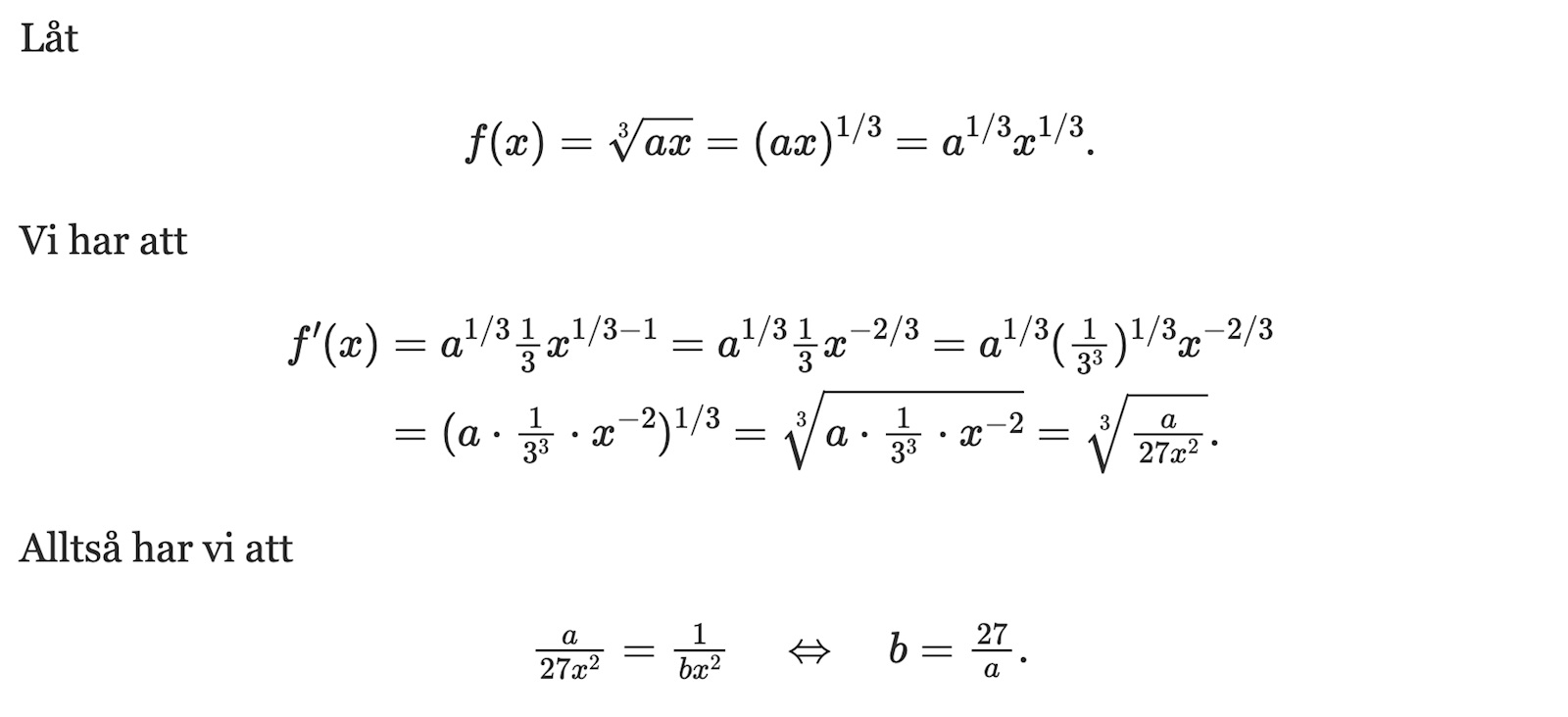
Så omvägen att ha (1/3^3)^1/3 är alltså nödvändig för att få rätta svaret, jag förstår. Vad ska jag tänka på om en sån här fråga kommer på prov tror du? Då jag inte tänker på att ta en omväg? 

Squarerootofconfused skrev:

Så omvägen att ha (1/3^3)^1/3 är alltså nödvändig för att få rätta svaret, jag förstår. Vad ska jag tänka på om en sån här fråga kommer på prov tror du? Då jag inte tänker på att ta en omväg? 

n:te-roten som skrivsätt

var populärt på tidigt 1900-tal. Då hade man (på något sätt) "enklare" matematik och inte derivator och så mycket potensregler som idag. Den beteckningen är ofta av ondo idag. Det ser snyggt och "stiligt" ut, men den är rätt värdelös att räkna effektivt med.

Använd alltid

för här kan du lätt räkna med potenslagar m.m. 

Här får man mentalt tänk till lite om man tänker som "på gamla tiden"

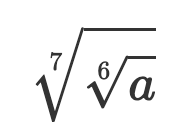
medan

vilket jag tycker är enklare och snabbare att räkna med

Se bara på

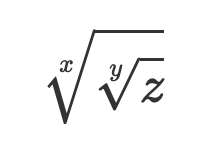
det är mkt. enklare att hantera

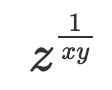
Den här videon ligger nog lite över din nivå för tillfället, men tittar gärna på den och se hur rottecknen reduceras till enkel multiplikation och addition och man kommer lättare fram till svaret

https://www.youtube.com/watch?v=GMisAdN1VhY

Squarerootofconfused skrev:

Men jag får dock fortfarande inte rätta svaret, jag får b=3/a^1/3 men svaret ska vara b=27/a.

Ja nu ser jag. Du råkade plocka bort ^1/3 från b:et (och då gjorde jag oxå det..). Lös istället

a^1/3/3=1/b^1/3

Tack så mycket! Nu fattar jag