Generaliserade integraler
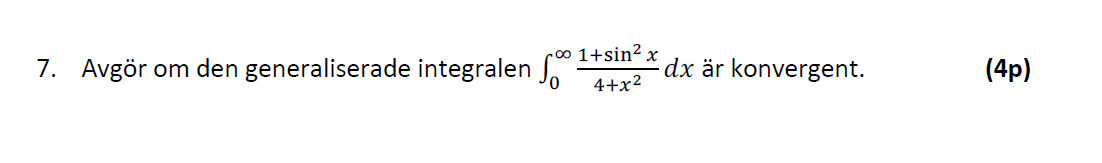
Facit:

Fel i facit! Borde inte jämförelse vara
Vad menar du med att sin^2(x) går mot 1 när x går mot oändligheten?
Dracaena skrev:Vad menar du med att sin^2(x) går mot 1 när x går mot oändligheten?
Stämmer det inte??
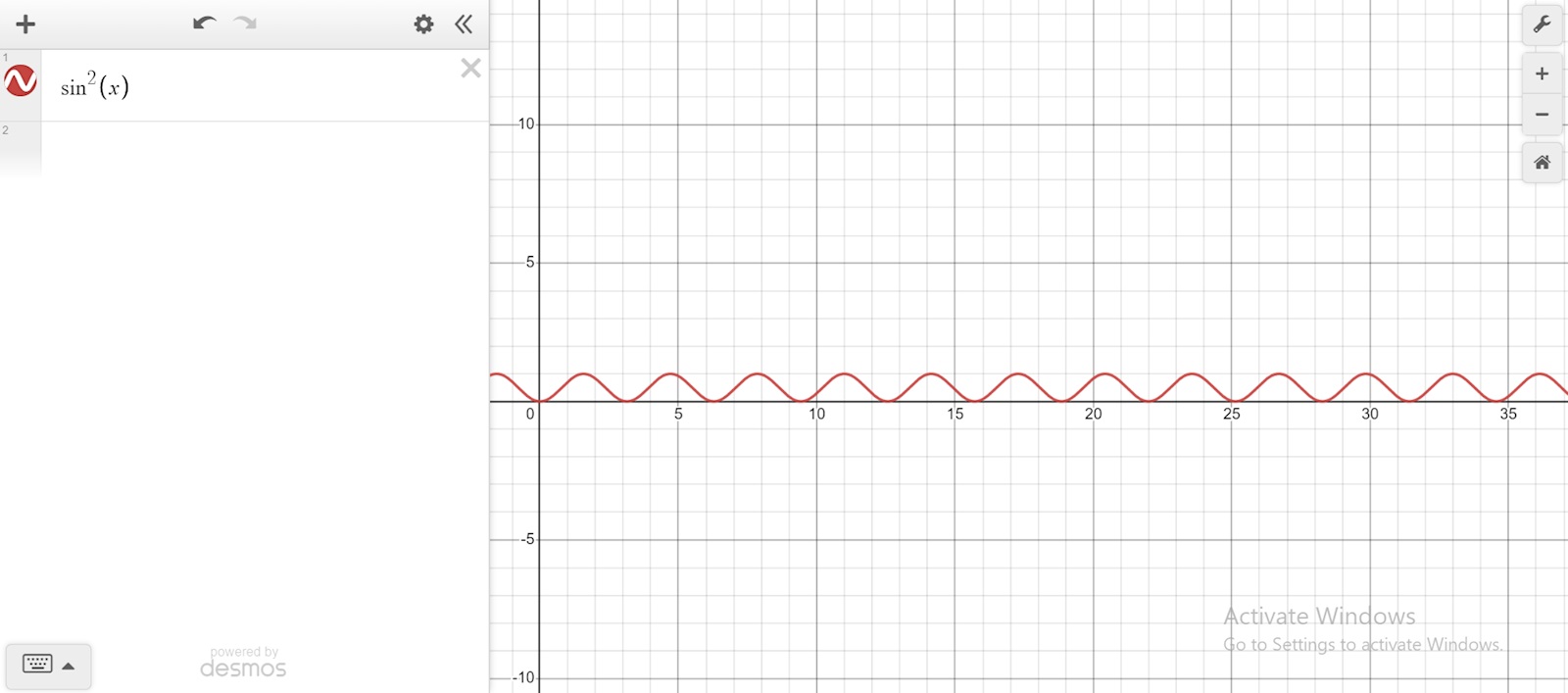
Oh right. y-värde varierar mellan 0 och 1. SÅ det kanske inte går emot exakt 1.
sin (x) divergerar när x går mot oändligheten. Men du har rätt, facit har missat det. Kommer dock fortfarande konvergera
ItzErre skrev:sin (x) divergerar när x går mot oändligheten. Men du har rätt, facit har missat det. Kommer dock fortfarande konvergera
Varför kommer den fortfarande kovergerar??
Marcus N skrev:ItzErre skrev:sin (x) divergerar när x går mot oändligheten. Men du har rätt, facit har missat det. Kommer dock fortfarande konvergera
Varför kommer den fortfarande kovergerar??
är inte divergent. Vi sa att = divergent
Detta kommer dock inte spela någon roll eftersom sinus är en begränsad funktion och påverkar inte om integralen konvergerar eller divergerar. För att bevisa att integralen är konvergent måste vi stänga in den mellan två integraler som båda är konvergenta.
stämmer det?
ItzErre skrev:
är inte divergent. Vi sa att = divergent
Detta kommer dock inte spela någon roll eftersom sinus är en begränsad funktion och påverkar inte om integralen konvergerar eller divergerar. För att bevisa att integralen är konvergent måste vi stänga in den mellan två integraler som båda är konvergenta.
Marcus N skrev:
stämmer det?
ser bra ut, är du med på att konvergerar?
Ja, man kan brytar ut konstanten 2 från integralen:
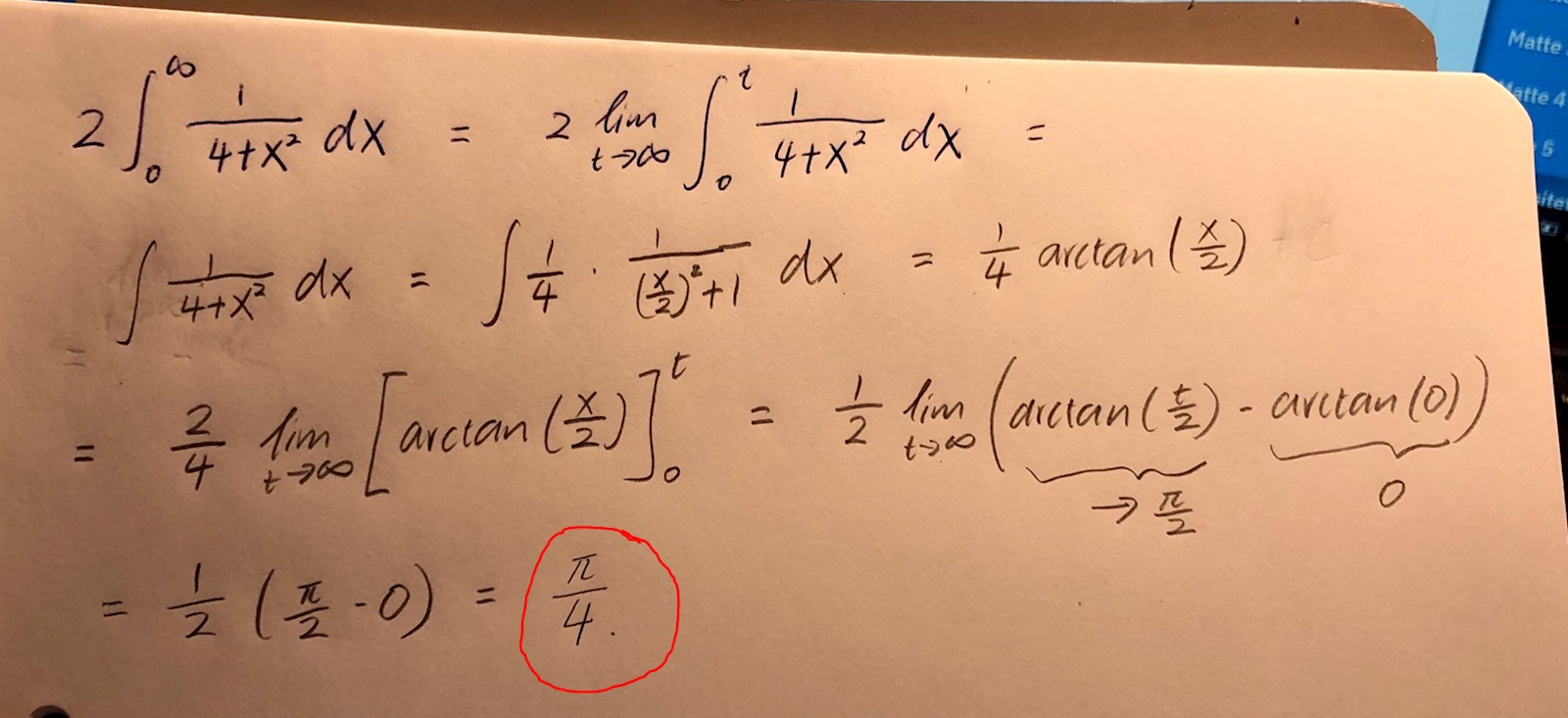
Du behöver inte räknar ut integralen, tex kan du jämföra med 1/x^2
Vad menar du att man kan jämföra med 1/x^2.
Jag har en sats här:
Men ja glömde hur man bevisar dem, kan ni förklarar detta?




