Generaliserad integral - hur hade ni löst denna?
Hejsan
Hur hade ni tänkt på denna integral:
?
Frågan är bara om den konvergerar eller divergerar.
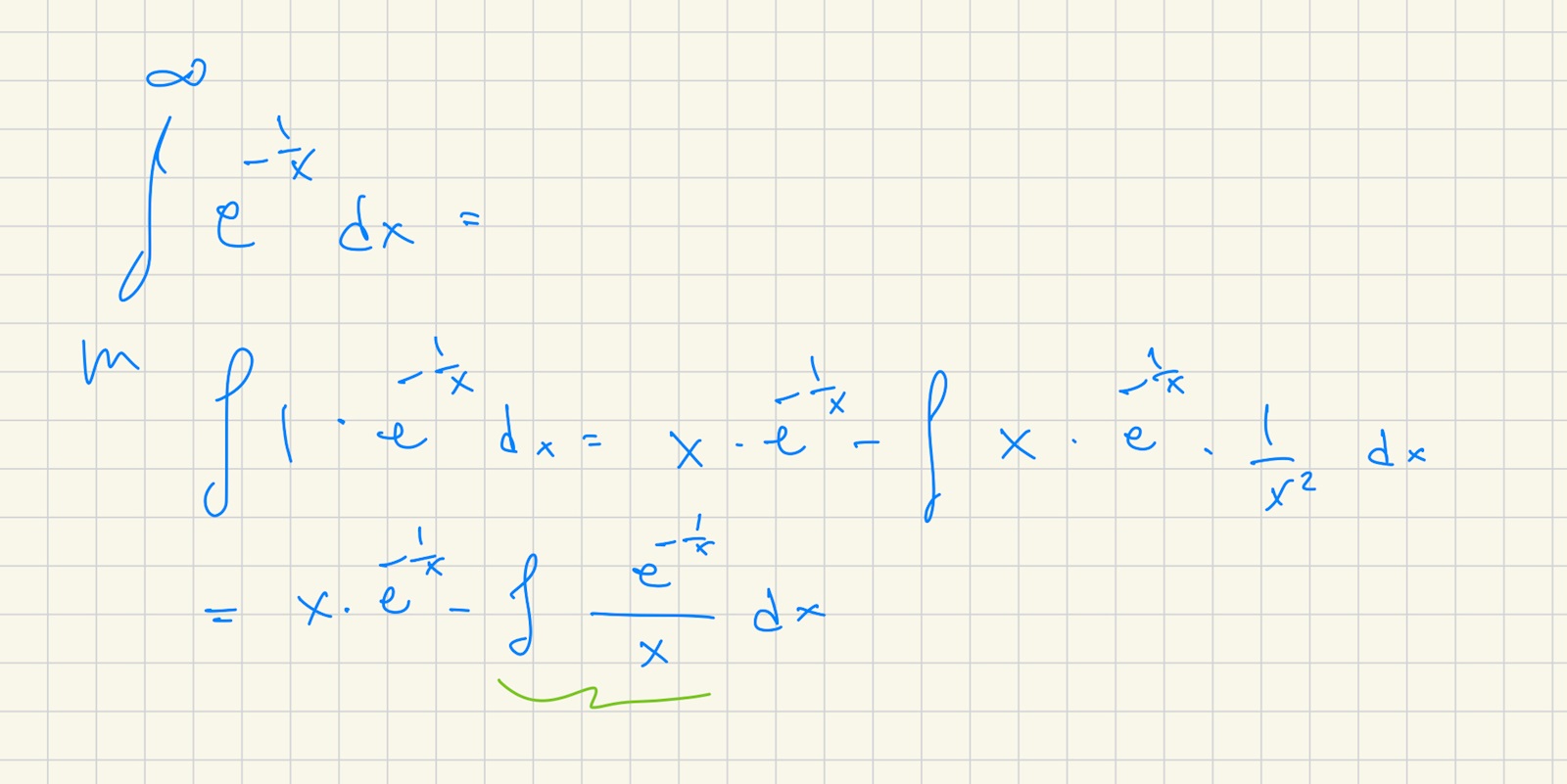
Ska man direkt kunna förstå efter en PI att den divergerar pga det grönmarkerade?
Ja, jag tycker det är fullt rimligt att man får anta det. Den grönmarkerade integralen (om man tar med minustecknet framför) är lika med (se mer här) och denna är definitivt divergent från till .
Det räcker att konstatera att:
tomast80 skrev:Det räcker att konstatera att:
Så enkelt var det ja.
Att jag inte hittade den jämförelsen själv är ganska sorgligt.
MrPotatohead skrev:tomast80 skrev:Det räcker att konstatera att:
Så enkelt var det ja.
Att jag inte hittade den jämförelsen själv är ganska sorgligt.
Övning ger färdighet... jag lärde mig detta efter 4,5 år på Teknisk Fysik. Gör många liknande uppgifter så ser du mönstrena till slut.
Ja man harvar ju på. Det ska nog gå bra. Tack för tipset iaf.
Rent allmänt-om integranden inte går mot noll då x går mot oändligheten så kommer integralen ALLTID vara divergent.
jamolettin skrev:Rent allmänt-om integranden inte går mot noll då x går mot oändligheten så kommer integralen ALLTID vara divergent.
Nja, hur menar du då?
Om integranden inte går mot noll då x går mot oändligheten, så kommer integralen att addera mer och mer area då x går mot oändligheten, alltså divergerar integralen.
Det lät ovanligt allmänt ja. Tack till er båda.
En enkel variant som fungerar är att om funktionen går mot ett gränsvärde så måste detta gränsvärde vara 0 för att integralen ska vara konvergent.





