Ge exempel på polynomfunktion av tredje graden
Hej!
Ge exempel på en polynomfunktion av tredje graden som
a) har två extrempunkter
b) saknar extrempunkter
Vet inte hur man ska komma fram till det riktigt. Jag kan sitta och testa mig fram tills jag snubblar över någonting kanske men.
Dkcre skrev:Hej!
Ge exempel på en polynomfunktion av tredje graden som
a) har två extrempunkter
b) saknar extrempunkter
Vet inte hur man ska komma fram till det riktigt. Jag kan sitta och testa mig fram tills jag snubblar över någonting kanske men.
Använd dig av derivatan. Hur många nollställen har derivatan i fall a och i fall b?
I a så 2 nollställen och i b inga nollställen alls.
Så.. Den ska skära x axeln på två ställen respektive inget alls. Jag gjorde det först men det var ändå svårt.
Eller jag tror den kan ha nollställen i b men ändå sakna extrempunkt ändå förresten..
Dkcre skrev:I a så 2 nollställen och i b inga nollställen alls.
Så.. Den ska skära x axeln på två ställen respektive inget alls. Jag gjorde det först men det var ändå svårt.
Derivatan av en tredjegradsfunktion är en andragradsfunktion. Hitta på en andragradsfunktion som har två (respektive noll) nollställen. Fundera ut en tredjegradsfunktion som hör ihop med den.
Eller jag tror den kan ha nollställen i b men ändå sakna extrempunkt ändå förresten..
Det stämmer, men varför välja ett krångligt exempel när man kan välja ett som är mindre krångligt?
Smaragdalena skrev:Dkcre skrev:I a så 2 nollställen och i b inga nollställen alls.
Så.. Den ska skära x axeln på två ställen respektive inget alls. Jag gjorde det först men det var ändå svårt.
Derivatan av en tredjegradsfunktion är en andragradsfunktion. Hitta på en andragradsfunktion som har två (respektive noll) nollställen. Fundera ut en tredjegradsfunktion som hör ihop med den.
Eller jag tror den kan ha nollställen i b men ändå sakna extrempunkt ändå förresten..
Det stämmer, men varför välja ett krångligt exempel när man kan välja ett som är mindre krångligt?
Okej.
för a så)
F'(x) = 3x^2 + 4x + 1 verkar ha två nollställen
Jag tror då att F(x) = x^3 + 2x^2 +x hör ihop bra med den.
Och för b:
f(x) = x^3 verkar fungera eftersom den bara har en terasspunkt och uppfyller då kraven..
Är det tillfredställande svar?
Rita upp funktionerna och kolla! Om du behöver mer hjälp: Lägg upp dina bilder här.
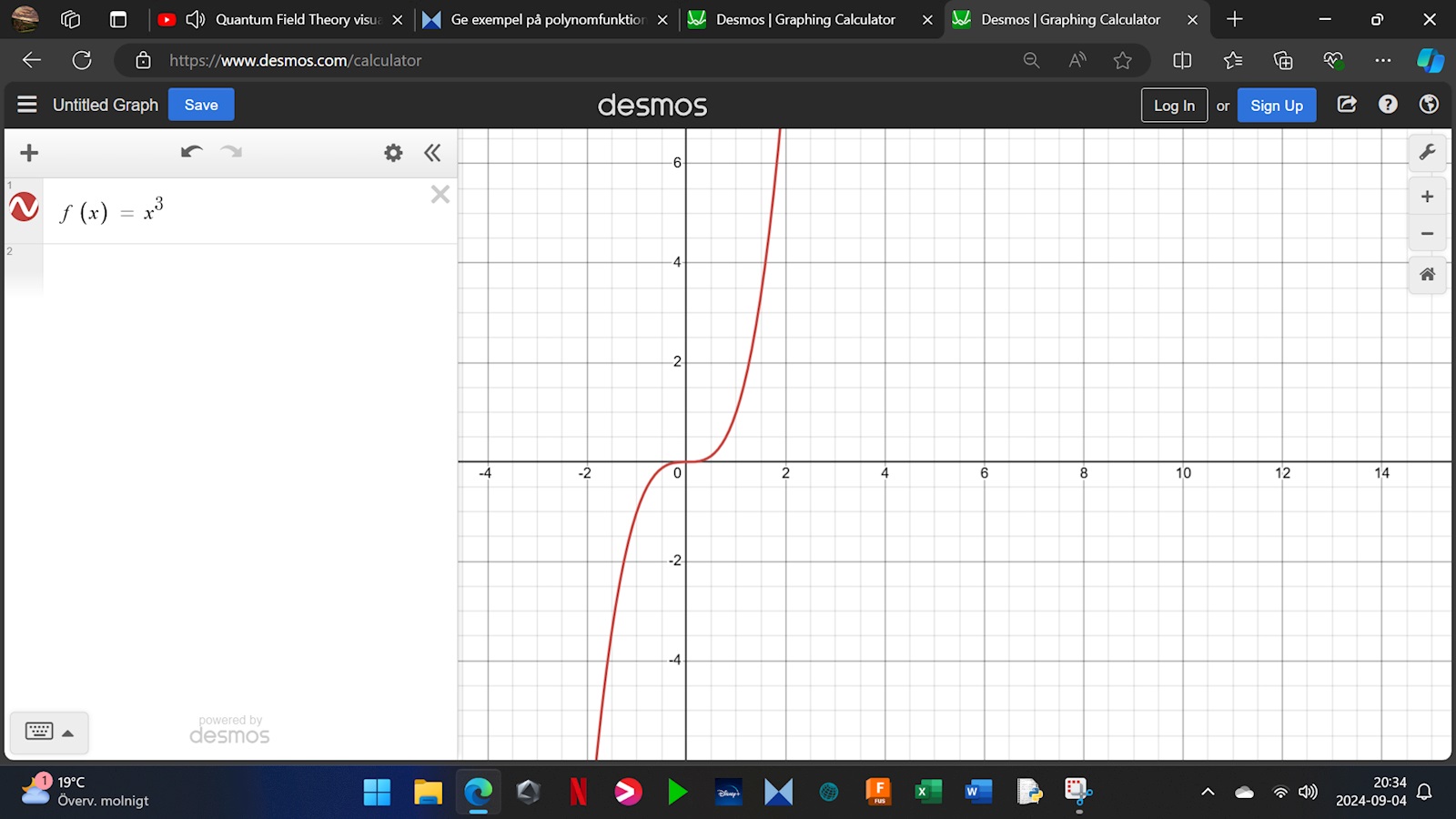
Okej, så för b:
 Och för a:
Och för a: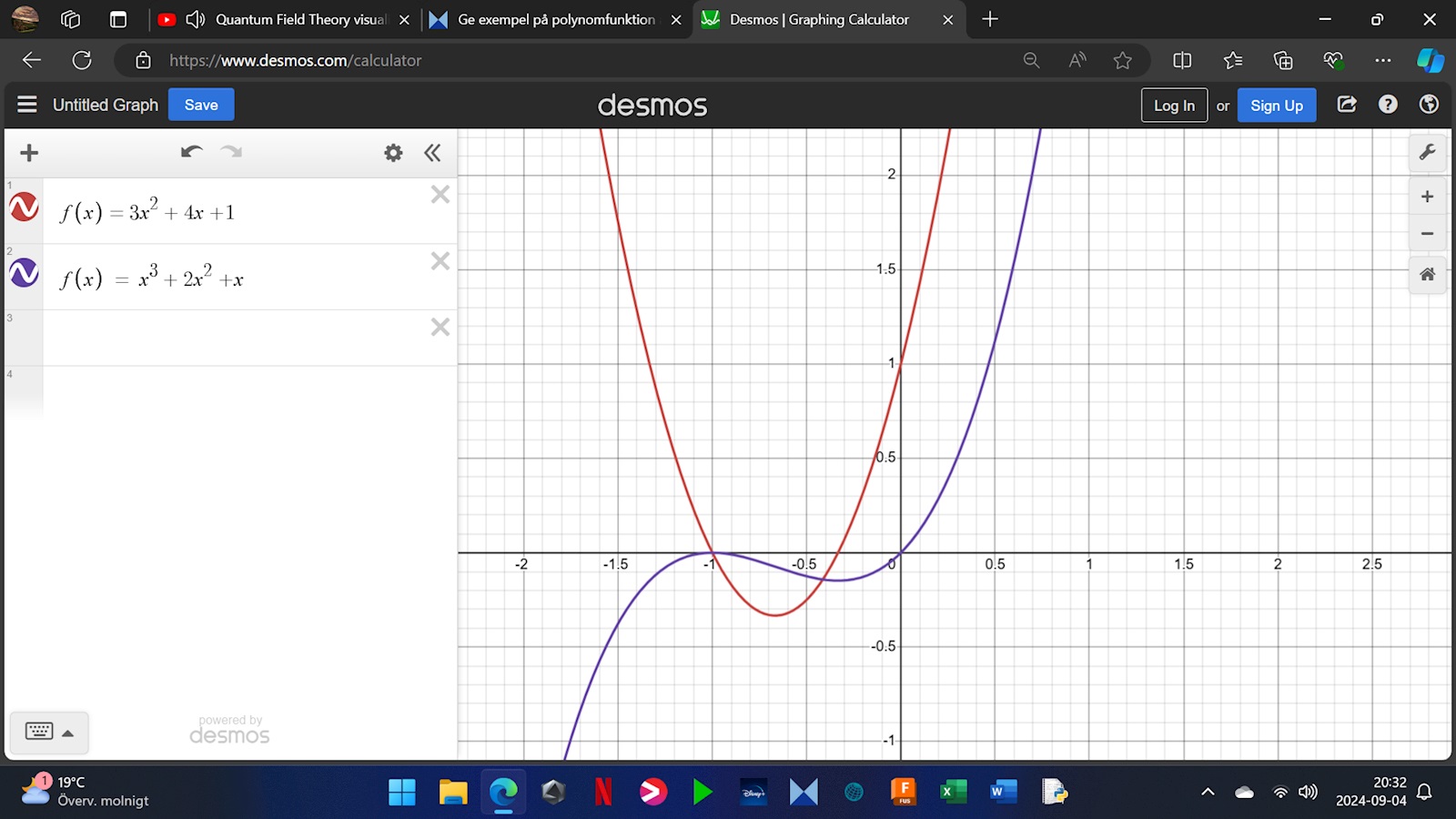
Snyggt!
Dkcre skrev:
Okej.
för a så)
F'(x) = 3x^2 + 4x + 1 verkar ha två nollställen
Jag tror då att F(x) = x^3 + 2x^2 +x hör ihop bra med den.
Och för b:
f(x) = x^3 verkar fungera eftersom den bara har en terasspunkt och uppfyller då kraven..
Är det tillfredställande svar?
Ja. Ännu bättre:
a) f(x) = x3+2x2+x, eftersom detivatan f'(x) = 3x2+4x+1 har två olika reella nollställen.
b) f(x) = x3, eftersom denna funktion endast har en terrasspunkt (i origo) och alltså ingen extrempunkt.
Så jag hade rätt alltså :) Tack så mycket. Det är svårt att svara på själv, man kan ju ha missuppfattat någonting och tror att man har rätt bara.




