Jag har inte provat själv. Har du? Är det dina anteckningar?
Först ville jag se en sinuskurva, men för NP är det nog överkurs.
Då såg jag två trianglar istället där vi vet tillräckligt för att använda likformighet.
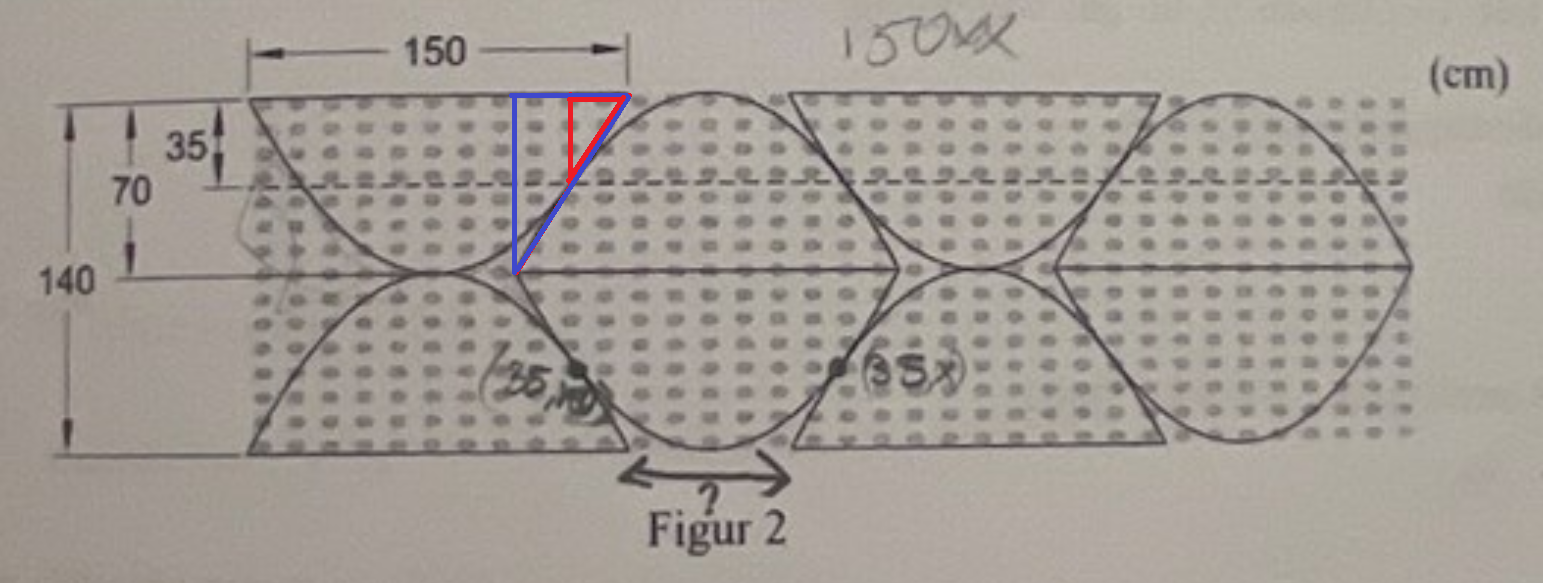
När vi vet korta kateten av den blå är vi hemma och kan räkna ut längden av tygstycket.
Gör ett försök!
Det är matte 2 så tror inte det är sinus eftersom vi jobbade med det i matte 1. Jag har försökt lösa den själv men vet ej vart jag ska börja
Vad tror du om min ansats med likformiga trianglar då?
Du vet längden av de långa kateterna och du vet hur de korta samt hypotenusorna förhåller sig till varandra.
hur menar du att man ska räkna då?
skolbuss skrev:hur menar du att man ska räkna då?
- Läs på om likformighet, nians matte.
- Korta kateten i blå triangeln är dubbla den rödas.
- Räkna ut den.
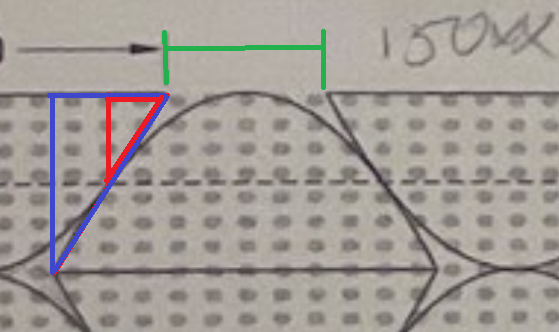
Sedan kan du beräkna det gröna avståndet jag markerat, vilket är allt du behöver för att lösa uppgiften.
Problem, svar och elevlösning ges här:
https://arkiv.edusci.umu.se/np/np-2-4-prov/Ma2c-ht14.pdf
Sid 32.
Dock är elevlösningen ej helt korrekt. Men facit bör vara rätt svar.
Nu när jag ser den publicerade lösningen, måste jag kanske göra en pudel här och inse att det inte går att lösa som jag tänkt. Vinkeln på tangenten gör att det finns oändligt många likformighetslösningar.
Man gör missar ibland, men det viktigaste är att försöka och ibland sedan inse att det är en återvändsgränd.
Tack! I elevlösningen så räknar de avståndet i mitten av parabeln, men varför ska man inte räkna avståndet där uppe istället? Det blir ju längre om man räknar i mitten
Jag hade räknat i mitten. Det är enklare och mera självklart. Jag fick längden till
225ROT(2)+150 ≈ 4.68 m

 hur ska man lösa denna uppgift?
hur ska man lösa denna uppgift?