Gammal Np derivata uppgift
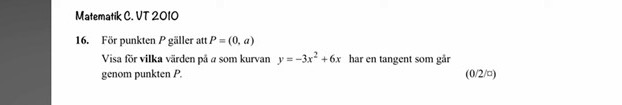
 Jag hittar inte facit till den här uppgiften så jag vet inte om jag är på rätt spår. Jag vet inte riktigt om jag ens fattar frågan
Jag hittar inte facit till den här uppgiften så jag vet inte om jag är på rätt spår. Jag vet inte riktigt om jag ens fattar frågan
Det ser ut som att du har fattat frågan rätt, även om jag själv gjorde på ett annat sätt. Det som blir fel i din uträkning är efter du har skrivit +a. Det man får efter att ha utvecklat det är
som ger , vilket innebär att a måste vara positivt.
Är då svaret a=3x^2 ?
Du har tänkt rätt, då a beräknas på det sättet av x. Dock så antar man att alla x är tillåtna då man följer x-axeln, så svaret borde vara alla positiva a.
Det jag inte fattar är vilka variabler jag borde använda. Är det ok att k=(-6x+6) i tangenten innehåller x och det är samma x som resten av tangenten innehåller eller borde de betecknas olika?
Det går bra att kalla båda fallen för x.
MiMia skrev:Det jag inte fattar är vilka variabler jag borde använda. Är det ok att k=(-6x+6) i tangenten innehåller x och det är samma x som resten av tangenten innehåller eller borde de betecknas olika?
Det är bättre att inte kalla två saker för samma namn, det blir så rörigt då. Kalla x-vädena för de båda tangeringspunkterna för t ex a respektive b. Då är tangeringspunkterna (a, -3a2+6a) respektive (b, -3b2+6b) och tangenternas k-värden är -6a+6 respektive -6b+6. Kommer du vidare härifrån?
Nu vet jag inte vad jag får fram Vad menar du med “båda” tangeringspunkterna? Är det inte bara en?
Vad menar du med “båda” tangeringspunkterna? Är det inte bara en?
Man ser på din bild i förstainlägget att det finns två tangeringspunkter, en med positivt och en med negativt x-värde. Det ser ju ut som om P är rakt ovanför maximipunkten. Därför trodde jag att det är två punkter. Det står också i uppgiften att man skall visa för vilka värden, inte vilket värde, på a som kurvan ...



