Gamla tenta frågan Ellära
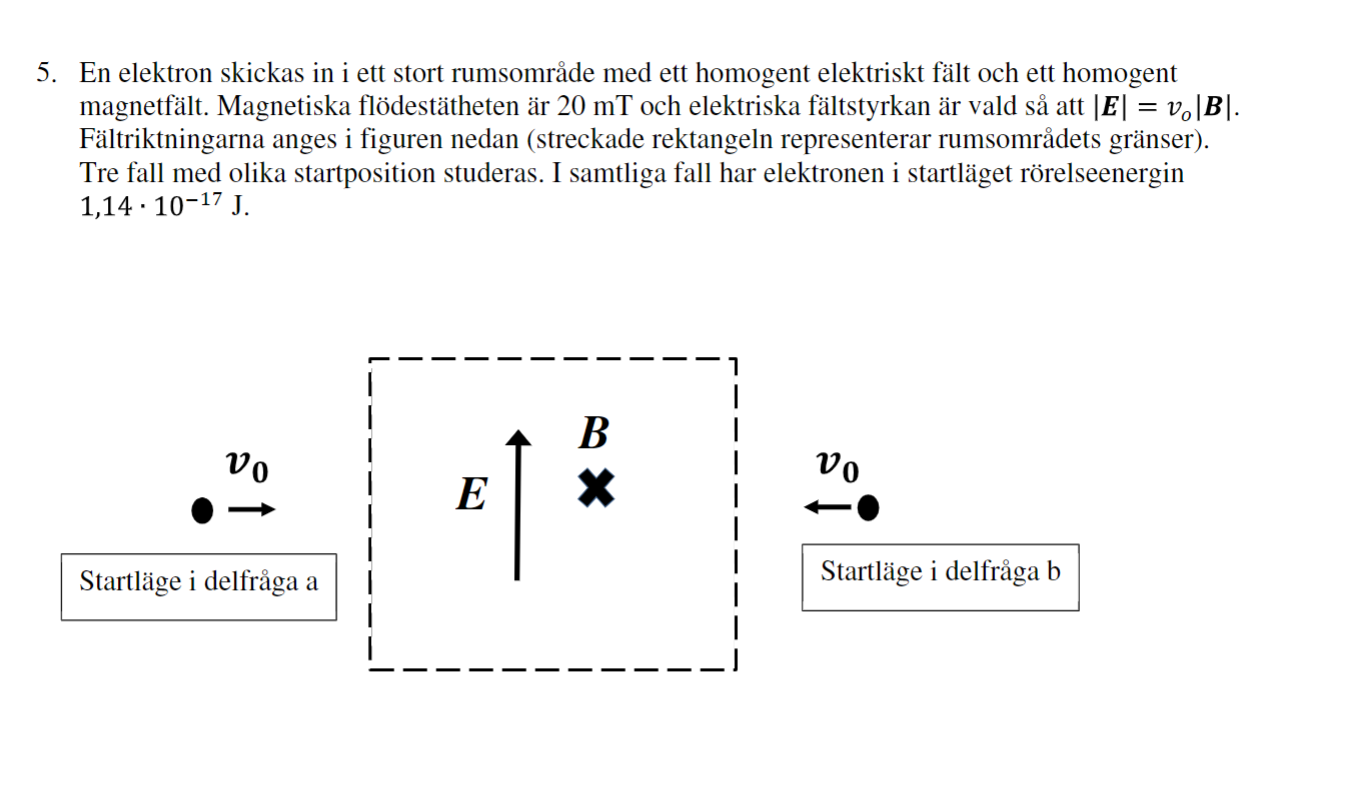

Facit för delfrågan a)

Varför är elektrisk kraften lika stora som magnetiskt kraften? Hur har dem fått värdet på v0? Varför är Fe och Fm samriktade och har riktningen (x) och varför sätter vi F(tot)=?
Det står i uppgiften att rörelseenergin från början är J
Sedan löser man ut ur formeln
Man har valt att sätta storleken på det elektriska fältet till , det står också i uppgiften. Det innebär att Lorentzkraften får två lika stora komponenter båda riktade åt samma håll vilket vi kan visa enligt följande:
Om vi låter peka uppåt längs papprets plan är
(Magnetfältet rakt in i pappret)
(Hastighet åt höger i bild)
Om du nu sätter in och beräknar med kryssprodukt (kom ihåg att ) ser du att såväl som är riktade i (negativ) -led (kom ihåg att är negativ). Storleken för var och en blir
.
Du kan också använda någon högerregel du lärt dig i gymnasiet för att hitta riktningarna. Tänk då på att elektronen är en negativ partikel.
F är det sammanlagda kraften, eller hur?
I förklaringen nämnde du något som Lorentzkraften och det har ja inte gått igenom, så vet inte vad det är för nåt.
På den här mening "Det innebär att Lorentzkraften får två lika stora komponenter båda riktade åt samma håll vilket vi kan visa enligt följande" förstår ja inte!
Men ja kan förstår att man kan beräkna den sammanlagd elektromagnetiska kraften så här:
F=q(v×B+E) den här uttrycket känner jag igen.
Sen har ja inte gått igenom tecken som . Och ja har inte heller gått igenom kryssprodukten hittills. Så försök att undvika använda kryssprodukten när du förklarar lösningen.
I slutet nämnde du att man kan använda högerhandsregeln, det har ja läst mycket om. Men jag tror högerhandsregeln använder bara för magnetfältet och bestämma kraftriktningen för magnetkraften, hur kan vi bestämma kraftriktning på den elektriskt kraftens riktningen?
Marcus N skrev:F är det sammanlagda kraften, eller hur?
Ja, den sammanlagda kraften består av två delar. den magentiska kraften och kraften från E-fältet
I förklaringen nämnde du något som Lorentzkraften och det har ja inte gått igenom, så vet inte vad det är för nåt.
Lorentzkraften är just , dvs
I den ingår en kryssprodukt för att bestämma den magentiska kraften
Eftersom facit hänvisar till Lorentzkraften med kryssprodukt antog jag att ni hade gått igenom det.
I slutet nämnde du att man kan använda högerhandsregeln, det har ja läst mycket om. Men jag tror högerhandsregeln använder bara för magnetfältet och bestämma kraftriktningen för magnetkraften, hur kan vi bestämma kraftriktning på den elektriskt kraftens riktningen?
E-fältet påverkar laddningen med en kraft som är riktad i E-fältets riktning och ges av
I det här fallet är E-fältet riktat uppåt och vi har en negativ partikel, alltså är riktad nedåt.
Magnetkraftens riktning kan du få genom att sätta tummen motriktad , dvs åt vänster (eftersom partikeln är negativt laddad är strömmen motriktad rörelsen) och pekfingret riktad i magnetfältets riktning (in i pappret). Då vill handflatan trycka partikeln nedåt (alternativt långfingret pekar nedåt).
Magnetkraftens storlek är
Okej, så Lorentzkraften => elektromagnetiska kraften i ett området.
Nej, vi har aldrig räkant med kryssprodukt hittills för att alla uppgifter som vi har haft är magnetfältet alltid vinkelrätt med hastigheten.
Jag har läst mycket om högerhandsregeln så jag håller med dig och facit när ni säger Fm kommer riktar nedåt.
Men när det kommer till bestämma kraftriktningen i en elektriskt fältet då känner jag inte lika hur man ska utförar.
Är det så här kanske:
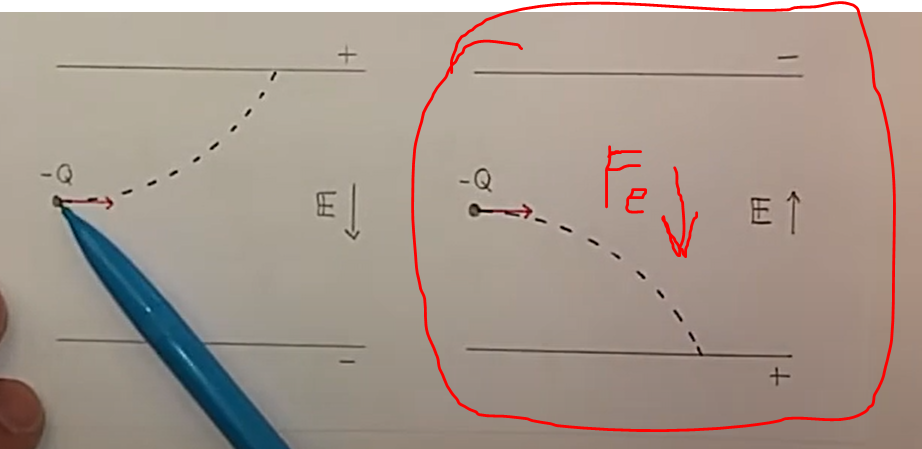
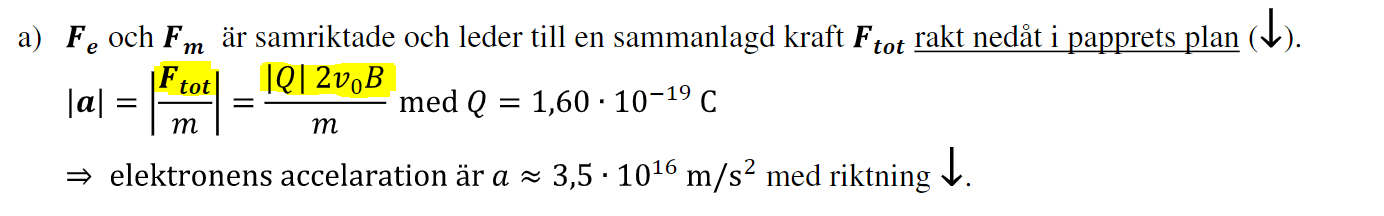
Varför är Ftot beräknade så här i facit? Vet du?
Din bild stämmer bra. E-fältet är riktat från + till - och en negativ partikel böjer av mot plushållet.
Både och är riktade nedåt och lika stora
(nedåt)
(nedåt)
Alltså är
(nedåt)
I b):

Fe och Fm är motriktade för att Fe kommer pekar uppåt och Fm pekar nedåt, eller hur?
Nej, det är den magnetiska kraften , som byter riktning enligt högerregeln. Den elektriska kraften vill fortfarande dra elektronen nedåt. De två krafterna balanserar varandra, resultaten blir 0.
Du har rätt.
På c):


Varför är Fm=0 när partikelns rörelse är parallellt med magnetfält riktning?
Det är den del av hastigheten som är vinkelrät mot magnetfältet som ger upphov till kraften.
I de fall du räknat på är hastigheten och magnetfältet vinkelräta mot varandra och du kan då använda "hela" hastigheten utan att dela upp hastigheten i komposanter.
Men om det är en vinkel mindre än 90 grader mellan hastigheten och magnetfältet måste du dela upp hastigheten i en del som är vinkelrät mot magnetfältet och en del som är parallellt med magnetfältet.
När , dvs när hastigheten och magnetfältet är parallella finns det ingen del av hastigheten som är vinkelrät mot magnetfältet och kraften är därför 0.
D4NIEL skrev:Det är den del av hastigheten som är vinkelrät mot magnetfältet som ger upphov till kraften.
I de fall du räknat på är hastigheten och magnetfältet vinkelräta mot varandra och du kan då använda "hela" hastigheten utan att dela upp hastigheten i komposanter.
Men om det är en vinkel mindre än 90 grader mellan hastigheten och magnetfältet måste du dela upp hastigheten i en del som är vinkelrät mot magnetfältet och en del som är parallellt med magnetfältet.
När , dvs när hastigheten och magnetfältet är parallella finns det ingen del av hastigheten som är vinkelrät mot magnetfältet och kraften är därför 0.
Kan man sammanfattar detta som en tumregel: om partikeln sätts i rörelse parallellt med B då är accelerationen på partikeln genom B-fältet alltid noll. Och partikeln kommer fortsätta rakt in i B-fältets riktning med oförändrad hastighet och rörelseenergi.
Ja, så kan du sammanfatta det.
Som överkurs kan du också pränta in
Kryssproduktens storlek ges av produkten av storleken av och gånger sinus för mellanliggande vinkel
När mellanliggande vinkel är noll, dvs när B-fältet och rörelsen är parallella, blir produkten 0.
Kryssproduktens riktning ges av högerhandsregeln.


