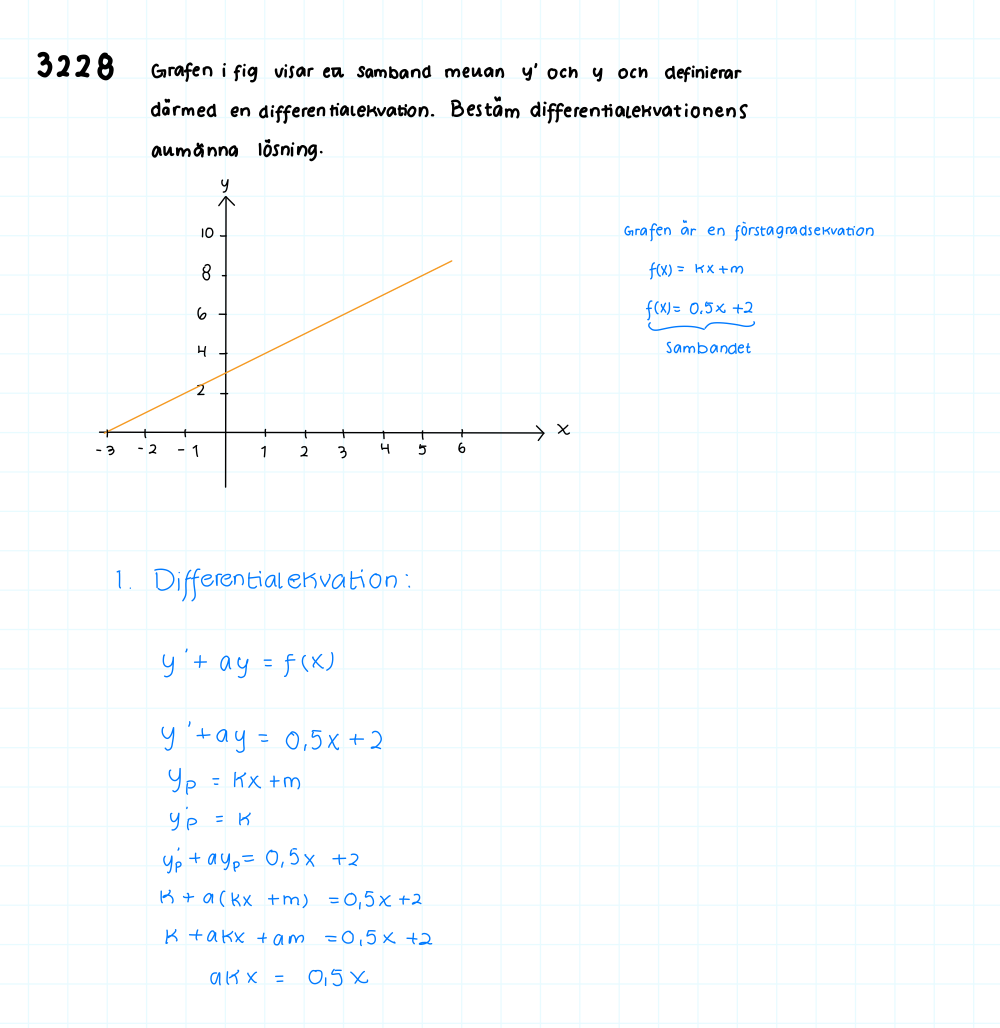
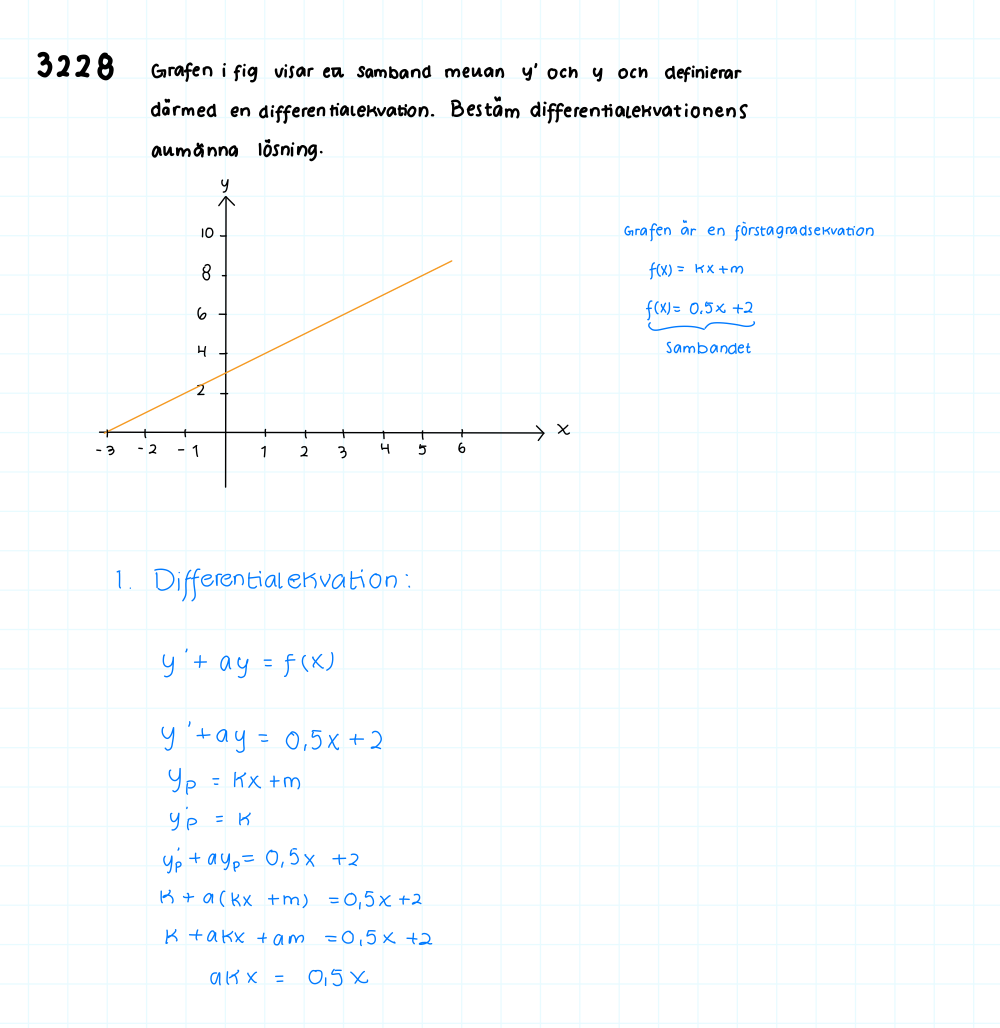
Gafen visar ett samband mellan.....
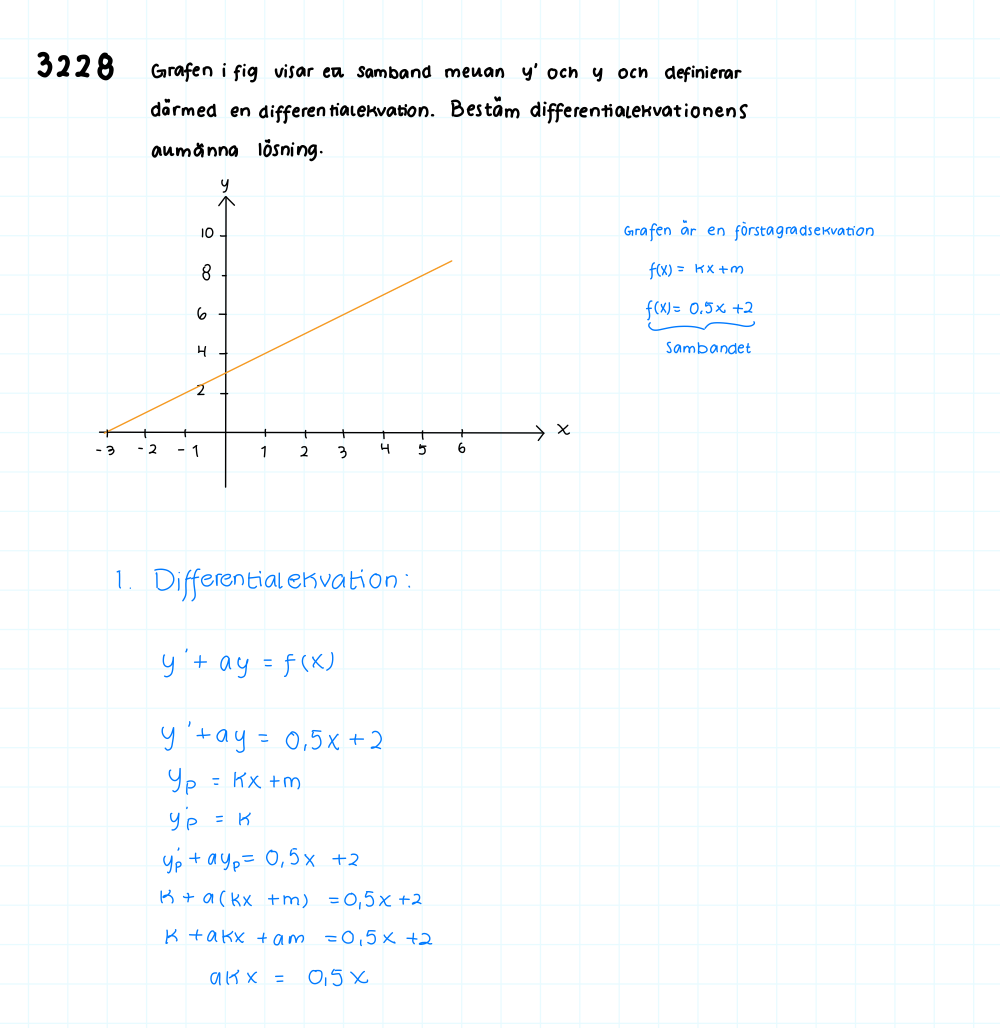
jag tänkte senare att
sista stegets HL är ju kx så om jag byter ut det får jag
akx=kx
a=1
vet inte om detta är rätt. Jag har ju flera okända så har ingen anning om hur jag ska bestämma den allmänna lösningen
fysik3 skrev:
jag tänkte senare att
sista stegets HL är ju kx så om jag byter ut det får jag
akx=kx
a=1
vet inte om detta är rätt. Jag har ju flera okända så har ingen anning om hur jag ska bestämma den allmänna lösningen
Nu har du tagit fram partikulärlösningen f(x) = x. Vad behöver du veta mer för att ta fram ALLA lösningar till diffekvationen?
Smaragdalena skrev:fysik3 skrev:
jag tänkte senare att
sista stegets HL är ju kx så om jag byter ut det får jag
akx=kx
a=1
vet inte om detta är rätt. Jag har ju flera okända så har ingen anning om hur jag ska bestämma den allmänna lösningen
Nu har du tagit fram partikulärlösningen f(x) = x. Vad behöver du veta mer för att ta fram ALLA lösningar till diffekvationen?
så det är rätt att a=1? detta kommer alltså ge mig att yp = x
då kan jag bestämma den homogena lösningen
yh= Ce-x?
sedan vet jag också att
y = yh+yp
vilket inte stämmer överens med facits svar :( fattar inte vart det går snett
Jag tror att jag missförstod uppgiften, den är så konstigt skriven. Enligt det blåa till höger visar grafen inte själva funktionen utan funktionens derivata. Då är partikulärlösningen "en primitiv funktion till y' = 0,5x+2".
jag hänger inte riktigt med f(x) beskriver ettt samband mellan y' och y så om vi skulle formulera en differentialekvation bör det vara y'+ay=f(x)
Vad säger facit?
Problemformuleringen är konstig. De säger att bilden visar ett samband mellan y och y', och i bilden är det x och y på axlarna, alltså inget samband alls mellan y och y'. Om det stode y respektive y' i stället, så skulle sambandet vara y' = 3 + y/3.
men gud ja det ska stå y' och y på axlarna, oj mitt fell hörni tack så mycket ska fortsätta