Fyrhörningens area
Hejsan! Behöver hjälp med en uppgift som lyder:
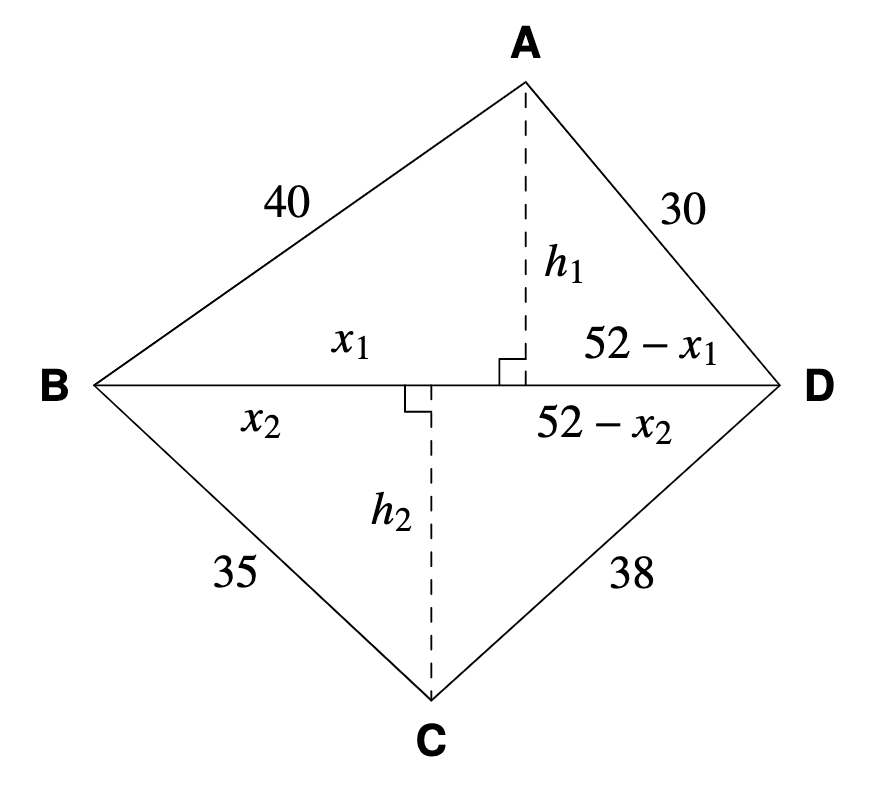
En fyrhörning ABCD har sidlängderna AB = 40 cm, BC = 35 cm, CD = 38 cm och DA = 30 cm. Dessutom är diagonalen BD = 52 cm. Hur stor är fyrhörningens area?
Jag har ritat upp en bild på fyrhörningen:
Vad skulle jag kunna börja med?

Det som man får göra är att räkna ut arean på båda trianglarna var för sig. Det kan man göra genom att hitta en vinkel i båda trianglarna genom cosinussatsen. När man har en vinkel i vardera triangel kan man använda areasatsen för att beräkna arean.
Kan det vara vilken vinkel som helst?
Ja, det spelar ingen roll vilken.
Skulle du kunna visa hur det ser ut när man använder cosinussatsen för att jag har lite problem med att veta hur den fungerar tack :)
Du hittar cossinussatsen i formelbladet för Matte 3:

I bilden har jag markerar vinkeln u i uppgiftens övre triangel:

Här ser vi att
- cm
- cm
- cm
- är den okända vinkeln
Cosinussatsen ger oss då
Ok tack ska jag göra samma sak för andra sidan och sedan addera ihop dem?
Nej, uppgiften gäller att beräkna fyrhörningens area.
Därför ska du beräkna arean av den övre triangeln (med hjälp av areasatsen) och arean av den undre triangeln (även här med hjälp av areasatsen) och sedan summera dessa areor.
Som du ser i formelbladet så använder areasatsen en vinkel och det är därför du först använder cosinussatsen för att beräkna vinklarna.
Jag får arean till 1440 cm2 men det är fel
Abulfazl skrev:Jag får arean till 1440 cm2 men det är fel
Visa hur du räknar så hjälper vi dig att hitta felet.
Ok så jag började med att lösa ut vinkeln (u) ur ekvationen du gav fick den ungefär till 94,9o och sedan för den undre triangeln samma sak sedan använde jag areasatsen och adderade summorna.
Abulfazl skrev:Ok så jag började med att lösa ut vinkeln (u) ur ekvationen du gav fick den ungefär till 94,9o och sedan för den undre triangeln samma sak sedan använde jag areasatsen och adderade summorna.
94,9° stämmer.
Hur beräknade du resten?
Visa gärna även själva uträkningarna så blir det både enklare och snabbare.
Det blir 'snyggare' svar med Pythagoras' sats.
Hur tänker du att man kan använda Pythagoras här?
Övre triangel:
Undre triangel:
Jag sitter fast här jag har bestämt en vinkel (v) som blev 90,8o
Abulfazl skrev:Övre triangel:
Nej, om du tittar på formeln för areasatsen så är
- cm, dvs längden av en av sidorna som utgår från vInkeln.
- cm, dvs längden av den andra sidan som utgår från vInkeln.
- , dvs vinkeln.
Du ska alltså använda formeln så här:
Undre triangel:
Jag sitter fast här jag har bestämt en vinkel (v) som blev 90,8o
EDIT - jag räknade fel här. Det ska vara ungefär 90,8°, se nedan.
Hur räknade du då? Jag får den till ungefär 90,6°.
Visa uträkningarna och inte bara resultatet av uträkningarna. Då kommer det att gå snabbare att hjälpa dig.
Yngve skrev:Hur tänker du att man kan använda Pythagoras här?

522 = 382 + 352 - 2 * 38 * 35 * cos (v)?
Abulfazl skrev:522 = 382 + 252 - 2 * 38 * 35 * cos (v)?
Varifrån kommer talet 25?
Menade 35
OK, hur ser fortsättningen ut?
Ställde du inte upp den så?
Abulfazl skrev:Ställde du inte upp den så?
Jo, men jag vill veta hur du fortsatte att räkna fram att v var ungefär lika med 90,8°.
Det stämmer nämligen inte.
Btw räknade även jag fel tidigare, vinkeln blir ungefär 90,1°
Jag får tydligen 104o?
382 + 352 - 2 * 38 * 35 * cos (v) = 522
1444 + 1225 - 2660cos(v) = 2704
2669 - 2660cos(v) = 2704
- 2660cos(v) = 2704 - 2669
- 2660cos(v)/-2660 = 35/-2660
cos (v) = -1/76
v = (- 1/76)-1 = 76
180o - 760 = 104o?
Abulfazl skrev:Jag får tydligen 104o?
382 + 352 - 2 * 38 * 35 * cos (v) = 5221444 + 1225 - 2660cos(v) = 2704
2669 - 2660cos(v) = 2704
- 2660cos(v) = 2704 - 2669
- 2660cos(v)/-2660 = 35/-2660
cos (v) = -1/76
Allt stämmer fram hit
v = (- 1/76)-1 = 76
Men det här är fel.
Om cos(v) = a så är v = +/- arccos(a)
I det här fallet får vi v = +/- arccos(-1/76), vilket är ungefär lika med +/- 90,8°
180o - 760 = 104o?
Och varför subtraherar du resultatet ftån 180°?
Jag tror att du blandar ihop det ned att ekvationen sin(v) = a har lösningarna v = arcsin(a) och v = 180°-arcsin(a).
Jaha men då var det ju 90,8o
Abulfazl skrev:Jaha med då var det ju 90,8o
Ja, det stämmer.
Jag ber om ursäkt, räknade fel tidigare
Nu fick jag till det till 1261 cm2 vilket var rätt tack för hjälpen Yngve :)
Trinity2 skrev:
Aha, OK så kan man också göra.
@Abdulfazl, pröva gärna även den metoden och avgör själv vilken du gillade bäst.