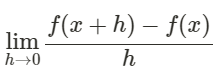Funktionen f(x)=x^2. Bestäm tangentens ekvation då x=2 (Matematik/Matte 3/Derivata)

Du vill ha tangentens ekvation, inte bara dess lutning. Då vill du ha något på formen y=kx+m.

fner skrev:
Du vill ha tangentens ekvation, inte bara dess lutning. Då vill du ha något på formen y=kx+m.

Alltså om x=2 så är f(2)=x^2 = 4?

Det är vårat k värde på y=kx+m eller?

så y=4x+m

Men vi behöver beräkna m för att få hela ekvationen?

Hur?

Men jag ser fortfarande ingen användning med detta:

Att derivera uttrycket f(x)=x^2

=> f'(x) = 2x

(vet inte ens hur man ändrar en funktion till ett deriverings uttryck, för jag fick 4x på tangentens lutning och inte 2x)

Du har beräknat tangentens lutning korrekt genom att ta f'(x)=2x och sedan stoppa in x=2 och få k=f'(2)=4.

Hittills vet vi alltså att y=4x+m.

För att få ut m måste vi ha en koordinatpunkt som vi vet att tangenten går igenom. Vi vet att tangenten går genom x=2, eftersom det är där den tangerar kurvan. y-värdet i x=2 kan du få genom att stoppa in x=2 i den ursprungliga funktionen, dvs f(2)=2²=4.

Nu vet vi att 4=4*2+m, och du kan lösa ut m.

fner skrev:
Du har beräknat tangentens lutning korrekt genom att ta f'(x)=2x och sedan stoppa in x=2 och få k=f'(2)=4.

f'(x) = 2x fick jag från boken, jag trodde man skulle använda f(x) = x^2, men det är ju inte samma sak som f'(x) = 2x?

Det är just detta som antar som en del av vad jag inte förstår

Rita.

fner skrev:
.

För att få ut m måste vi ha en koordinatpunkt som vi vet att tangenten går igenom.

Nu vet vi att 4=4*2+m, och du kan lösa ut m.

Är vi ute efter m då x=0? inte x=2? Jag trodde m var då x=0? Men du kanske menar m som att då x=2 antar värdet y?

Laguna skrev:
Rita.

Måste väl finnas en beräknings metod för att ta reda på tangentens lutning = 2?

Men om tangentens lutning är = 2 så varför är f(2) = 2^2 = 4 en lutning?

Jaha, 4 är inte en lutning det är bara y värdet för punkten den tangerar

Kan ni visa hur man beräknar tangentens lutning?

f(2) är inte en lutning, f(2) är y-värdet när x=2.

k=f'(2)

fner skrev:
f(2) är inte en lutning, f(2) är y-värdet när x=2.

hur får man fram lutningen hos tangenten med funktionen f(x) = x^2?

fner skrev:

Du har beräknat tangentens lutning korrekt genom att ta f'(x)=2x och sedan stoppa in x=2 och få k=f'(2)=4.

Hittills vet vi alltså att y=4x+m.

Vad står detta för då? Är inte 4x en lutning =4?

Tangentens lutning är 2 eller 4?

f'(x)=2x är grafens lutning i varje given x-koordinat. Vi vet att vi har en tangent i x=2 och vi vill därför ha grafens lutning (=tangentens lutning) i den punkten. Vi sätter alltså in x=2 så att vi får f'(2)=2*2=4. Tangentens lutning är således 4.

fner skrev:
f'(x)=2x är grafens lutning i varje given x-koordinat. Vi vet att vi har en tangent i x=2 och vi vill därför ha grafens lutning (=tangentens lutning) i den punkten. Vi sätter alltså in x=2 så att vi får f'(2)=2*2=4. Tangentens lutning är således 4.

Jaha ok, så om vi har funktionen f(x) = x^2, måste man rita den för att veta att den har lutningen 2x vid varje punkt? Eller går det att beräkna på något sätt?

Vet du hur man hittar derivatan av en funktion? Hur långt har ni kommit på genomgångarna? Det känns märkligt att ni skulle få en sådan här fråga utan att veta hur man deriverar...

fner skrev:
Vet du hur man hittar derivatan av en funktion? Hur långt har ni kommit på genomgångarna? Det känns märkligt att ni skulle få en sådan här fråga utan att veta hur man deriverar...

Jag kan ta bilder av genomgångs sidorna så kan du see om jag behöver kunna detta, eller om det är något annat jag måste kunna inför provet kanske?

Om du orkar läsa ungefär 4 sidor ksk

Det kan vara lite mixat eftersom jag fick denna fråga från eddler.se

Har ni pratat om derivatans definition? Om inte så tror jag tanken är att ni ska rita funktionen och tangenten.

fner skrev:
Har ni pratat om derivatans definition? Om inte så tror jag tanken är att ni ska rita funktionen och tangenten.

Jag kan ta bilder snabbt för att visa

Kanske tar nya bilder, dem var suddiga

Jag skulle säga att utifrån teorin ni har gått igenom så är den "rätta vägen att gå" att rita upp funktionen och tangenten i x=2 och få k-värdet därifrån.

fner skrev:
Jag skulle säga att utifrån teorin ni har gått igenom så är den "rätta vägen att gå" att rita upp funktionen och tangenten i x=2 och få k-värdet därifrån.

Måste man använda gränsvärde för att få f(x)=x^2 => derivatansfunktion f'(x)=2x?

Ja precis. Ni kommer att börja med "derivatans definition":

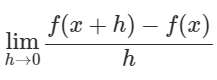
Om du vill kan du testa med funktionen i uppgiften.

fner skrev:
Ja precis. Ni kommer att börja med "derivatans definition":

Om du vill kan du testa med funktionen i uppgiften.

Jaha, så måste vi då tänka på att funktionen kommer vara en glad mun, alltså x^2 går mot oändligheten uppåt? så lim blir lim x=>oändligheten+?

Men om man får k värdet givet i frågan, måste man då beräkna derivatansfunktion?

Såhär skulle du använda derivatans definition, men kom ihåg att du inte förväntas kunna detta än!!!

$\lim_{h \to 0} \frac{{(x + h)}^{2} - x^{2}}{h} = \lim_{h \to 0} \frac{x^{2} + 2 x h + h^{2} - x^{2}}{h} = \lim_{h \to 0} \frac{h (2 x + h)}{h} = 2 x$

Om k-värdet är givet i uppgiften behöver du inte beräkna derivatan. Derivatan är ett annat ord för lutningen/k-värdet. Då räcker det att beräkna m-värdet.

fner skrev:
Såhär skulle du använda derivatans definition, men kom ihåg att du inte förväntas kunna detta än!!!

$\lim_{h \to 0} \frac{{(x + h)}^{2} - x^{2}}{h} = \lim_{h \to 0} \frac{x^{2} + 2 x h + h^{2} - x^{2}}{h} = \lim_{h \to 0} \frac{h (2 x + h)}{h} = 2 x$

vad är h för ngt? alltså x+h? Varför skriver man dem

Allt kommer klarna när ni går igenom det i skolan. h är bara ett godtyckligt x-värde. När h går mot noll betyder det att vi kommer närmre och närmre det x-värde man vill hitta tangenten i.

Är du nöjd med hjälpen för denna uppgiften? Derivator kommer klarna allt eftersom!

fner skrev:
Allt kommer klarna när ni går igenom det i skolan. h är bara ett godtyckligt x-värde. När h går mot noll betyder det att vi kommer närmre och närmre det x-värde man vill hitta tangenten i.

Är du nöjd med hjälpen för denna uppgiften? Derivator kommer klarna allt eftersom!

jag är självstuderande

fner skrev:
Såhär skulle du använda derivatans definition, men kom ihåg att du inte förväntas kunna detta än!!!

$\lim_{h \to 0} \frac{{(x + h)}^{2} - x^{2}}{h} = \lim_{h \to 0} \frac{x^{2} + 2 x h + h^{2} - x^{2}}{h} = \lim_{h \to 0} \frac{h (2 x + h)}{h} = 2 x$

Jag ser, h går bort eftersom det är onödigt att skriva så små värden med många decimaler eller hur?

(2x+h)=2x

h går bort pga det, annars skulle det inte vara godtyckligt.

Men vad om h=>2

h går alltid mot 0 i den här formuleringen av derivatan. h är inte ett x-värde, utan en liten skillnad mellan två x-värden.

Laguna skrev:
h går alltid mot 0 i den här formuleringen av derivatan. h är inte ett x-värde, utan en liten skillnad mellan två x-värden.

Ja, vad om det stod t.ex x=> 4 eller h=>4?

Jag har redan lärt mig en hel del om när man beräknar derivatans definition. Men typ bara för h=>0, vad är bra att tänka på när det gäller t.ex lite mer avancerade uttryck då x=>4 eller h=>4?

Det andra sättet att skriva derivatans definition är $f'(x_0) =\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}$ .

Laguna skrev:
Det andra sättet att skriva derivatans definition är $f'(x_0) =\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}$ .

så om det stod typ h=4 då x=7, betyder det att f'(x) går mot x=7 med ett närmevärde

När skulle det stå h = 4? h går mot 0.

Laguna skrev:
När skulle det stå h = 4? h går mot 0.

Det är bara ett exempel jag tar fram. När h=>4 då är gränsvärdet/derivatans punkt x=7.00001?

Ställ upp ett helt uttryck och visa vad du menar. h går inte mot 4 i de situationer jag har beskrivit.