Funktionen

Jag antar att du menar att du har ritat upp funktionen till och med att x=3, dvs. till och med f(3).

För att ta reda på vad som händer då x=3 så konstaterar vi att det är den nedre av de två formlerna som används för att räkna ut funktionsvärdet då x=3, då dess definitionsmängd är då x är större än eller lika med 3. Stoppa därför bara in att x=3 i den nedre formeln.

För att ta reda på vad som händer då x=6 så konstaterar vi att det är den nedre av de två formlerna som används för att räkna ut funktionsvärdet då x=6, då dess definitionsmängd är då x är mindre än eller lika med 6. Stoppa därför bara in att x=6 i den nedre formeln.

Då du skriver att du ritat "graferna" trots att det bara kommer bli en graf till den här funktionen undrar jag om du kanske missuppfattat uppgiften något.

Tack så mycket för ert svar. Jag har gjort till det du skrev men sen när jag vill rita f(x+3) i samma koordinatsystem det är då jag menar vad som händer när x= 3 och x=6?

H

Vad är uppgiften? Är det bara att rita upp funktionen, eller är det något annat?

Att rita de två funktionerna plus f(x+3) i ett koordinatsystem.

Att rita funktionen av x+3 är likvärdigt med att säga att alla värden som vi stoppar i funktionen kommer bli tre värden större innan vi stoppar in i en av de två formlerna.

f(x+3) kommer om man ritar upp det bli likadan som f(x) fast förskjuten med 3 i x-led.

Då x=3 i f(x+3) kommer du få f(3+3)= f(6) vilket kan räknas ut av den nedre formeln eftersom den gällde då det som man tar funktionen av är mindre än eller lika med 6, och 6 är mindre än eller lika med 6.

ERMI skrev:

Att rita de två funktionerna plus f(x+3) i ett koordinatsystem.

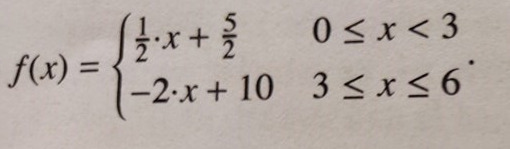
Vilka två funktioner? Det är bara en funktion, fast den har olika definition i olika interfall.