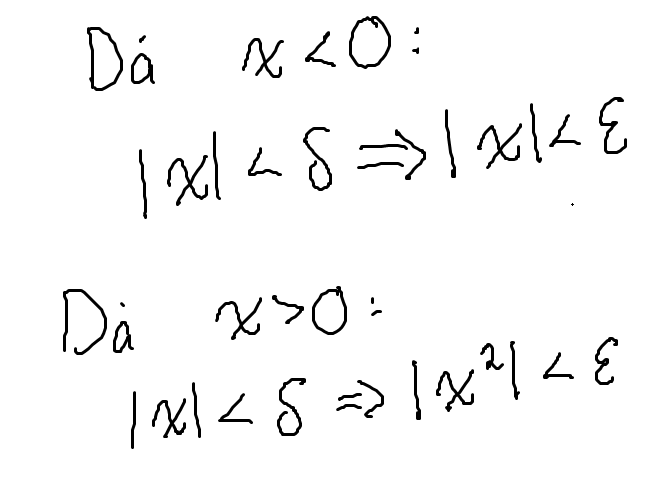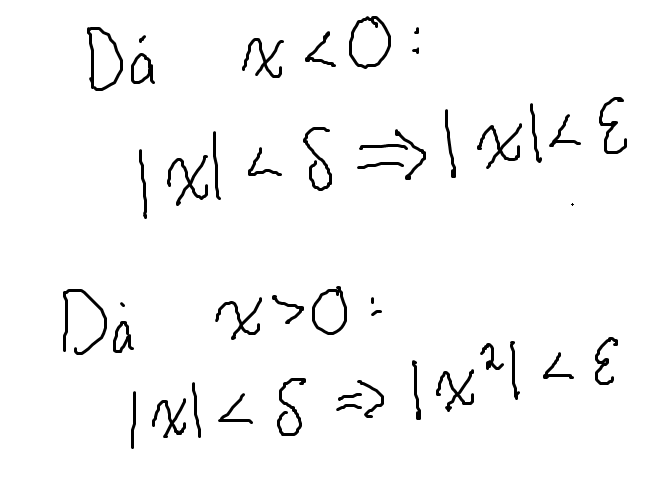Funktion har gränsvärde 0

Vilken definition ska du använda? Den klassiska epsilon-delta definitionen eller den där satsen?

naytte skrev:

Vilken definition ska du använda? Den klassiska epsilon-delta definitionen eller den där satsen?

Den här satsen!

Men satsen ovan uttalar sig väl endast om huruvida ett gränsvärde existerar, inte vad det är lika med?

naytte skrev:

Men satsen ovan uttalar sig väl endast om huruvida ett gränsvärde existerar, inte vad det är lika med?

Det fanns en lite liknande uppgift som använt satsen, så jag tänkte att man tillämpar den även i denna?

Jo precis, i den uppgiften skulle man bara visa att ett gränsvärde inte fanns. Nu ska vi inte bara visa att gränsvärdet finns, utan dessutom att det är lika med noll. Det verkar inte som om sats 3.1.16 är tillämpbar här. Står det att man ska använda sats 3.1.16 i uppgiften?

naytte skrev:

Jo precis, i den uppgiften skulle man bara visa att ett gränsvärde inte fanns. Nu ska vi inte bara visa att gränsvärdet finns, utan dessutom att det är lika med noll. Det verkar inte som om sats 3.1.16 är tillämpbar här. Står det att man ska använda sats 3.1.16 i uppgiften?

Nej, du har rätt. Det står inte utskrivet vilken sats man ska använda. Den här har vi oxå:

Men gud vilka lustiga satser. Detta är bara en omformulering av den gängse definitionen av gränsvärdet (som jag rekommenderar att du använder här). Man säger att $f$ har ett ändligt gränsvärde $L$ i punkten $x=a$ om och endast om

$\displaystyle (\forall \epsilon>0)(\exists \delta>0)(\forall x\in D_f \setminus \{a\})[|x-a|<\delta\implies |f(x)-L|<\epsilon]$

Försök använda denna definition istället (om det är tillåtet). Sätt $L = 0$ och tänk på vilka två fall vi får (ett fall då x<0 och ett då x>0).

naytte skrev:

Men gud vilka lustiga satser. Detta är bara en omformulering av den gängse definitionen av gränsvärdet (som jag rekommenderar att du använder här). Man säger att $f$ har ett ändligt gränsvärde $L$ i punkten $x=a$ om och endast om

$\displaystyle (\forall \epsilon>0)(\exists \delta>0)(\forall x\in D_f \setminus \{a\})[|x-a|<\delta\implies |f(x)-L|<\epsilon]$

Försök använda denna definition istället (om det är tillåtet). Sätt $L = 0$ och tänk på vilka två fall vi får (ett fall då x<0 och ett då x>0).

Ja, det var den jag tänkte, jag är mer van med att använda epsilon än m ändå. Men kunde jag visa skillt för båda f(x) och även f(0)? 

$f(0)$ kan vi högaktningsfullt strunta i här eftersom vi tittar på alla $x$-värden förutom $x=a$. Om jag förstår dig rätt tänker du nog rätt. Ställ upp hur det ser ut då $x<0$ och när $x>0$.

naytte skrev:

$f(0)$ kan vi högaktningsfullt strunta i här eftersom vi tittar på alla $x$-värden förutom $x=a$. Om jag förstår dig rätt tänker du nog rätt. Ställ upp hur det ser ut då $x<0$ och när $x>0$.

Så här började jag:

Som sagt är sats 3.1.16 inte passande här. Jag tänkte att du skulle ställa upp det så här:

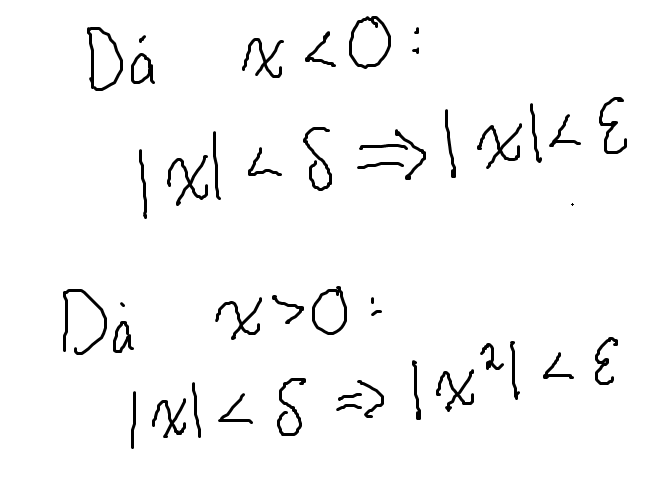
Låt $\varepsilon$ vara givna i de två fallen. Låt oss betrakta fallet då $x< 0$ först. Vad skulle vi möjligtvis kunna välja för $\delta$ sådant att implikationen alltid är sann?

naytte skrev:

Som sagt är sats 3.1.16 inte passande här. Jag tänkte att du skulle ställa upp det så här:

Låt $\varepsilon$ vara givna i de två fallen. Låt oss betrakta fallet då $x< 0$ först. Vad skulle vi möjligtvis kunna välja för $\delta$ sådant att implikationen alltid är sann?

okej, tack för förklaringen. Om delta=epsilon? Är det ju alltid sant, eller?

filippahog skrev:

naytte skrev:

Som sagt är sats 3.1.16 inte passande här. Jag tänkte att du skulle ställa upp det så här:

Låt $\varepsilon$ vara givna i de två fallen. Låt oss betrakta fallet då $x< 0$ först. Vad skulle vi möjligtvis kunna välja för $\delta$ sådant att implikationen alltid är sann?

okej, tack för förklaringen. Om delta=epsilon? Är det ju alltid sant, eller?

Och sorry, det här är väl rätt definition:

okej, tack för förklaringen. Om delta=epsilon? Är det ju alltid sant, eller?

Japp, precis.

Nu måste vi hitta ett $\delta$ givet ett fixt $\varepsilon$ så att den andra implikationen alltid är sann. Kan du lösa det?

Och sorry, det här är väl rätt definition:

Japp, det ser det ut att vara.

naytte skrev:

okej, tack för förklaringen. Om delta=epsilon? Är det ju alltid sant, eller?

Japp, precis.

Nu måste vi hitta ett $\delta$ givet ett fixt $\varepsilon$ så att den andra implikationen alltid är sann. Kan du lösa det?

Och sorry, det här är väl rätt definition:

Japp, det ser det ut att vara.

Jag kanske har helt fel. Men kan det vara att delta=epsilon i kvadrat?

Nästan, jag tänker att det borde bli $\sqrt{\varepsilon}$. Nu måste vi välja ett nytt delta, och då väljer vi helt enkelt det som är minst, alltså:

$\delta = \min\{\delta_1, \delta_2\} = \sqrt{\varepsilon}$

Nu har vi hittat ett delta > 0 som för vilket epsilon > 0 som helst gör att implikationen är sann. Alltså är vi klara.

naytte skrev:

Nästan, jag tänker att det borde bli $\sqrt{\varepsilon}$.

Ok. Men hur ska man komma vidare? Vi vet implikationerna men ska jag nu skriva m.h.a definitionen att det finns ett epsilon och delta som gör så att funktionen har ett gränsvärde?

Jag vet inte om mitt inlägg hann uppdateras innan du skrev ditt men som sagt väljer vi helt enkelt det delta som är minst av de vi har hittat. Om kravet är uppfyllt för ett visst delta kommer det såklart också vara uppfyllt för ett mindre :)

Hänger du med?

naytte skrev:

Jag vet inte om mitt inlägg hann uppdateras innan du skrev ditt men som sagt väljer vi helt enkelt det delta som är minst av de vi har hittat. Om kravet är uppfyllt för ett visst delta kommer det såklart också vara uppfyllt för ett mindre :)

Hänger du med?

Jag hoppas det.. :) I en fd uppgift valde vi delta att vara min( delta1,delta2). Ursäkta! Nu såg jag din uppdaterade kommentar. Exakt på samma sätt

filippahog skrev:

naytte skrev:

Jag vet inte om mitt inlägg hann uppdateras innan du skrev ditt men som sagt väljer vi helt enkelt det delta som är minst av de vi har hittat. Om kravet är uppfyllt för ett visst delta kommer det såklart också vara uppfyllt för ett mindre :)

Hänger du med?

Jag hoppas det.. :) I en fd uppgift valde vi delta att vara min( delta1,delta2). Ursäkta! Nu såg jag din uppdaterade kommentar. Exakt på samma sätt

Tusen tack för hjälpen. Du var till stor hjälp! Ha en bra kväll

Ingen orsak! Vad kul att det var till hjälp!