Funktion av två variabler, symetri med avseende på x och y

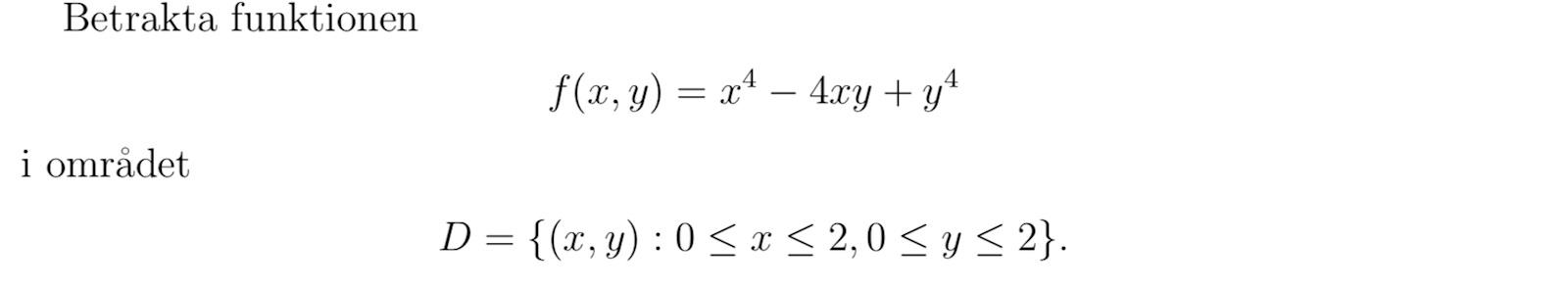
Eftersom att området D samt att funktionen är symmetrisk med avseende på x och y räknade det med att räkna ut två sidor och sedan spegelvända sidorna.

Jag försökte att testa runt lite med andra funktioner och visuellt ser det ut som att många funktioner är symmetriska med avseende på x och y. Kommer alla funktioner att vara symmetriska med avseende på x och y så längde som man göra samma sak med båda variablerna? Till exempel lägger till 4x^2y^2 så är den fortsatt systemisk? Jag testade att dela med xy och det som ut som att de fortsatt var symmetriska. Innebär det att jag kan lägga till hur många termer som helt så länge den innehåller lika många x som y:n?