Funktion av två variabler, kedjeregeln

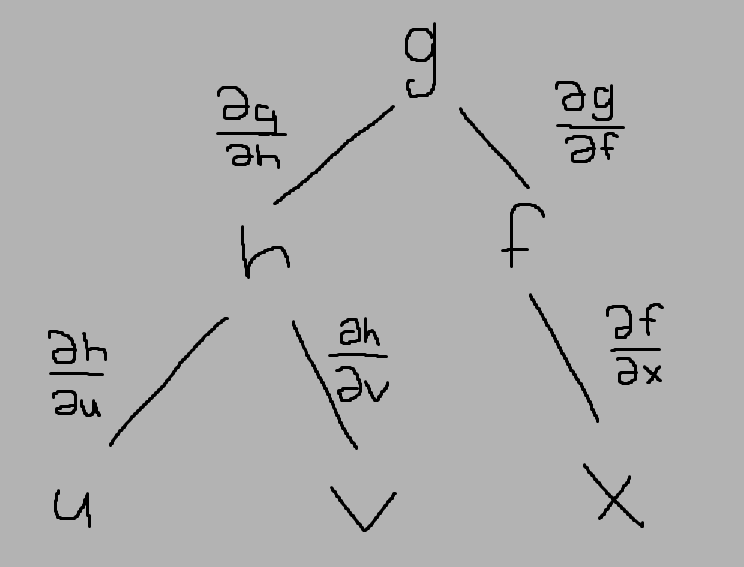
Tänk på att x är en funktion av h som är en funktion av u och v. Så även partiella derivatorna från detta håll måste med.

Calle_K skrev:

Tänk på att x är en funktion av h som är en funktion av u och v. Så även partiella derivatorna från detta håll måste med.

Vart kommer f’(x) in i bilden?

Derivera g med avseende på y (som är lika med f) sen applicerar du kedjeregeln igen, dvs deriverar f med avseende på x (som är lika med h) och sist derivera h med avseende på u

Calle_K skrev:

Derivera g med avseende på y (som är lika med f) sen applicerar du kedjeregeln igen, dvs deriverar f med avseende på x (som är lika med h) och sist derivera h med avseende på u

Jag missade att y=f(h(u,v)), ska försöka lösa igen nu när jag vet det lol

Calle_K skrev:

Derivera g med avseende på y (som är lika med f) sen applicerar du kedjeregeln igen, dvs deriverar f med avseende på x (som är lika med h) och sist derivera h med avseende på u

Kan jag lika gärna uttrycka lösningen så här?

$\dfrac{\partial z}{\partial u}=\dfrac{\partial g}{\partial h}\dfrac{\partial h}{\partial u}+\dfrac{\partial g}{\partial f}\dfrac{\partial f}{\partial h}\dfrac{\partial h}{\partial u}$

Yes, precis så skulle jag svarat

Calle_K skrev:

Yes, precis så skulle jag svarat

okej tack!