Funktion

Tänk grafiskt! Det största värdet kommer om funktionen har negativ derivata, eftersom det skulle innebära att vi gått nedåt när vi gått från noll till fem. Då kommer vi gå uppåt när vi går tillbaka. Den minsta möjliga derivatan i intervallet är f'(x) = -0,7. Vad händer om du går baklänges fem steg med den lutningen?

Smutstvätt skrev:

Tänk grafiskt! Det största värdet kommer om funktionen har negativ derivata, eftersom det skulle innebära att vi gått nedåt när vi gått från noll till fem. Då kommer vi gå uppåt när vi går tillbaka. Den minsta möjliga derivatan i intervallet är f'(x) = -0,7. Vad händer om du går baklänges fem steg med den lutningen?

 jag fattar inte :(

I situationer som denna är det väldigt bra att rita en bild! Du har ett värde för funktionen i en punkt, och sedan har du att dess derivata i ett intervall ligger mellan ett visst par värden.

Nu gäller det att inse att $f\left(5\right)$ ligger i slutet på intervallet $\left[0,5\right]$ och därför vill vi välja att derivatan skall vara $-0.7$ på hela intervallet. Varför vill vi det? Jo, vi noterar att om vi väljer en derivata $>0$ på hela intervallet så kommer $f\left(5\right)>f\left(0\right)$, men om vi väljer en derivata $<0$ på hela intervallet kommer $f\left(5\right)<f\left(0\right)$. Rita en bild för att se det. Sedan kan man snabbt inse att för att maximera $f\left(0\right)$ vill vi alltså välja det minsta värdet på derivatan vi kan (återigen, rita en bild).

EDIT: Wow jag är långsam, eller är det smutstvätt som är snabb?

Moffen skrev:

I situationer som denna är det väldigt bra att rita en bild! Du har ett värde för funktionen i en punkt, och sedan har du att dess derivata i ett intervall ligger mellan ett visst par värden.

Nu gäller det att inse att $f\left(5\right)$ ligger i slutet på intervallet $\left[0,5\right]$ och därför vill vi välja att derivatan skall vara $-0.7$ på hela intervallet. Varför vill vi det? Jo, vi noterar att om vi väljer en derivata $>0$ på hela intervallet så kommer $f\left(5\right)>f\left(0\right)$, men om vi väljer en derivata $<0$ på hela intervallet kommer $f\left(5\right)<f\left(0\right)$. Rita en bild för att se det. Sedan kan man snabbt inse att för att maximera $f\left(0\right)$ vill vi alltså välja det minsta värdet på derivatan vi kan (återigen, rita en bild).

 

EDIT: Wow jag är långsam, eller är det smutstvätt som är snabb?

Moffens svar förklarar väldigt bra. Börja med att läsa det svaret, och återkom om det fortfarande är oklart. :)

Moffen skrev:

I situationer som denna är det väldigt bra att rita en bild! Du har ett värde för funktionen i en punkt, och sedan har du att dess derivata i ett intervall ligger mellan ett visst par värden.

Nu gäller det att inse att $f\left(5\right)$ ligger i slutet på intervallet $\left[0,5\right]$ och därför vill vi välja att derivatan skall vara $-0.7$ på hela intervallet. Varför vill vi det? Jo, vi noterar att om vi väljer en derivata $>0$ på hela intervallet så kommer $f\left(5\right)>f\left(0\right)$, men om vi väljer en derivata $<0$ på hela intervallet kommer $f\left(5\right)<f\left(0\right)$. Rita en bild för att se det. Sedan kan man snabbt inse att för att maximera $f\left(0\right)$ vill vi alltså välja det minsta värdet på derivatan vi kan (återigen, rita en bild).

 

EDIT: Wow jag är långsam, eller är det smutstvätt som är snabb?

 men hur vet vi att om vi väljer en derivata större än noll på hela intervallet så kommer f(5) vara större än f(0)? och hur vet vi att om vi väljer en derivata som är mindre är noll på hela intervallet så kommer f(5) vara mindre än f(0) ??

Om derivatan är negativ lutar kurvan neråt, d v s om X > x så är f(X) < f(x).

Om derivatan är 0 lutar kurvan inte alls, d v s om X > x så är f(X) = f(x).

Om derivatan är positiv lutar kurvan uppåt, d v s om X > x så är f(X) > f(x).

Här en bild över situationen, med positiv respektive negativ derivata:

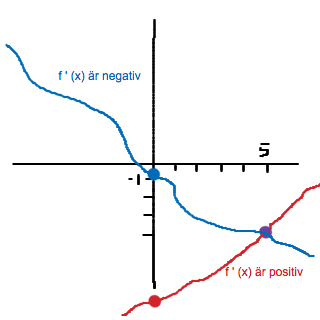
Den lila punkten är (5; -3,9) medan den röda och den blåa punkten är var x = 0:s y-värde skulle hamna.  (Som du märker är inte bild min starka sida... :D )