Fräsch härledning av uttrycket för arbete i ett kolv-cylinder-gas-system

Halloj!

Jag har under en längre period funderat över uttrycket för arbete under kompression/expansion av en gas i ett kolv-cylinder-system. Jag såg en härledning idag som jag tyckte var riktigt fräsch, så jag vill dela med mig av denna. Det som jag gillar är att det inte krävs mer än gymansiekunskaper i matematik för att hänga med. Vi börjar med en liten ritning av situationen:

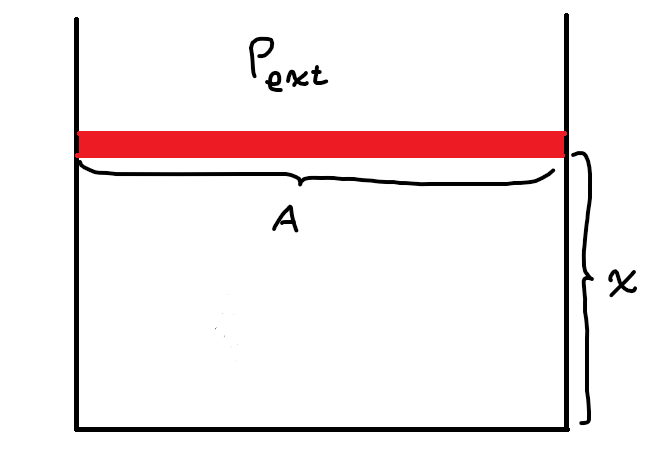
Det röda stycket är vår (friktionsfria) kolv av massa $m$ , som kan flytta sig upp och ned i gastuben, $A$ dess tvärsnittsarea, och där $x$ betecknar avståndet från denna till botten av kolven. $P_{\text{ext}}$ är omgivningens genomsnittstryck på kolven. Ur Newtons andra lag vet vi att:

$\displaystyle \textbf{F}_{\text{g}}+\textbf{F}_{\text{ext}}=m\textbf{a}=m\frac{dv}{dt}\hat{e}$

där $\textbf{F}_{\text{g}}=F_g \hat{e}$ är gasens kraft på kolven (och där $\hat{e}$ är enhetsvektorn i kraftens riktning). Det följer att vi dessutom har $\textbf{F}_{\text{ext}}=-P_{\text{ext}}A\hat{e}$ . Vi kan därför stryka vektorerna och enbart arbeta med skalärer:

$\displaystyle F_{\text{g}}-P_{\text{ext}}A=m\frac{dv}{dt}$

Om vi multiplicerar allting med kolvens fart $v$ erhåller vi:

$\displaystyle F_{\text{g}}v-P_{\text{ext}}Av=mv\frac{dv}{dt}$

Kolvens fart måste ju vara tidsderivatan av funktionen $x=x(t)$ . Dessutom måste $Av$ motsvara förändringen av volymen hos gasen med avseende på tid. Vi har således:

$\displaystyle F_{\text{g}}\frac{dx}{dt}-P_{\text{ext}}\frac{dV}{dt}=mv\frac{dv}{dt}$

Om vi gångrar allt med tidselementet $dt$ och sedan tillämpar integraloperatorn erhåller vi:

$\displaystyle w=\int_{x_i}^{x_f}F_{\text{g}}dx=\left[\frac{mv^2}{2}\right]_{v_i}^{v_f}+\int_{V_i}^{V_f}P_{\text{ext}}dV$

Om vi har att initialhastigheten för kolven är densamma som sluthastigheten (t.ex. $v_i = v_f = 0 \;\;\mathrm{ms^{-1}}$ har vi endast:

$\displaystyle w=\int_{V_i}^{V_f}P_{\text{ext}}dV$

vilket är det klassiska uttrycket.

Bara tyckte detta var lite coolt, så ville dela med mig. Jag hade ganska länge förundrats över varifrån denna formel kom (och t.ex. varför bara det yttre trycket spelade roll), och det var först idag som jag råkade snubbla in på denna härledning.

Jag tycker detta verkar oerhört tillkrånglat och försöker kringå fysikalisk förståelse med matematisk formalism.

Hela argumentet är 5 rader vars kontenta är att om kolven är i vila (eller har samma fart) i början och i slutet av kompressionen så har arbetet inte medfört någon nettoförändring i kolvens rörelseenergi. Ett faktum som inte kräver 5 ekvationer, och där denna infallsvinkel förskjuter vårt fokus från gasens fysik till fysiken hos ett artefakt.

Om vi förstår att arbetet i en sådan situation inte överför någon energi till kolven så är det väl uppenbart att arbetet måste ha utförts på gasen...?

Själva arbetetsberäkningen måste väl mycket lättare göras på det vanliga viset:

Arbete är ju bara kraft gånger sträcka. Om sträckan är liten, ds, så har vi

dW = F ds

utifall kraften kommer från ett tryck p** så kan vi skriva om

F = p A och inser att A*ds är lika med volymändringen

dW = F ds = p A ds = p dV

dW = p dV

Om trycket/kraften varierar under förflyttningen så får vi integralen

$W = \int_{V_i}^{V_f} pdV$

där tecken beror på konvention.

Jag förstår inte vad vi vinner med differentialekvationen.

Jag tycker detta verkar oerhört tillkrånglat och försöker kringå fysikalisk förståelse med matematisk formalism.

Det stämmer bra. Jag föredrar "matematiska härledningar" eftersom jag har svårt att förstå saker annars. Med en matematisk formalism (vissa antaganden, t.ex. att Newton II gäller) kan man komma fram till saker utan att förstå dem. Man kan lugnt och samsat stringent komma fram till rätt svar utan att förutsätta särskilt mycket alls. Jag har generellt svårt att förstå saker i fysiken, men om jag får läsa igenom en korrekt, matematisk härledning kan jag ändå acceptera dem, och det får väl ändå duga?

Jag förstår inte vad vi vinner med differentialekvationen.

Inte jag heller. Bara tyckte det var coolt.

Förresten, i din härledning är jag inte med på en sak. Vilket tryck är det vi tittar på här? Är det gasens tryck eller omgivningens tryck? Eller är det nettotrycket på kolven?

naytte skrev:

Förresten, i din härledning är jag inte med på en sak. Vilket tryck är det vi tittar på här? Är det gasens tryck eller omgivningens tryck? Eller är det nettotrycket på kolven?

Jag har inte härlett något specifikt. Jag har bara härlett den allmänna formeln för hur ett tryck på en plan yta resulterar i ett arbete när ytan sveper ut en volym när den rör sig parallellt med kraften. Det är allt formeln är.

Om du vill ha arbetet från nettokraft så är p en tryckskillnad.

Om du vill ha arbetet från ett yttre tryck så tar du yttre trycket.

Om du vill ha arbete som utförs på gasen så tar du gasens tryck.

Det vanligaste elementära sammanhanget där denna formel förekommer är i analysen av arbetscykler på gaser (så som Carnot eller Stirling-cykeln).

I det sammanhanget så är p trycket hos gasen i cylindern och inte det externa trycket (främst eftersom den yttre kraften inte nödvändigtvis kommer från en utspridd kraft). Skälet till det är dock att newtons lagar explicit säger oss att accelerationen under kompressionsförloppet är irrelevant för totala arbetets storlek så man kan lika gärna utgå från att den yttre kraften är lika stor som det som resulterar från det inte trycket. Dvs jämvikt F_ext = p_intern * A.

Ett perspektiv på din differentialekvation är att du kommer fram till att accelerationen är irrelvant för arbetet men detta är en grundläggande Kapitel 0 typ av kunskap och ska inte härledas om och om igen.

Svara

Visa senaste svar