Från funktion till annan funktion sen till graf är min tanke, men kanske finns de bättre sätt?

Du kan nyttja att x = (x-0), och där har du den formen du söker.

Har du lärt dig pq-formeln annars? Det är den oslagbart bästa metoden för att lösa ut rötter till andragradsfunktioner.

Hej, 
Menar du då att jag går från f(x)=-3x^2+12x till en funktion som jag kan plocka ut p värde och q värde som jag då vidare sätter in i pq? För testa att göra om f(x)=-3x^2+12x till pq, men fick då bara x^2-4x =0 ?

Det stämmer det du precis gjort. Återstår bara att lösa den sista ekvationen.

Tänk på att du inte går från en funktion till en annan. Det är samma funktioner, bara omskrivna på olika sätt.

okej, men hur får jag ett q värde, det går ju inte? betyder de att q=0

Stämmer bra

Okej, så om jag har räknat rätt får jag x1=0 och x2=0 

sätter jag in dessa värden i f(x)= a(x-x1)(x-x2)    typ  f(x)=a(x-0)(x-0) ..så.. betyder de att de finns 1 nollvärde & det är där x-axeln visar 0, dvs origo?  

Det ser fel ut. Hur använde du pq-formeln?

Du har rätt jag räkna fel. Räkna om & räknat då så här:

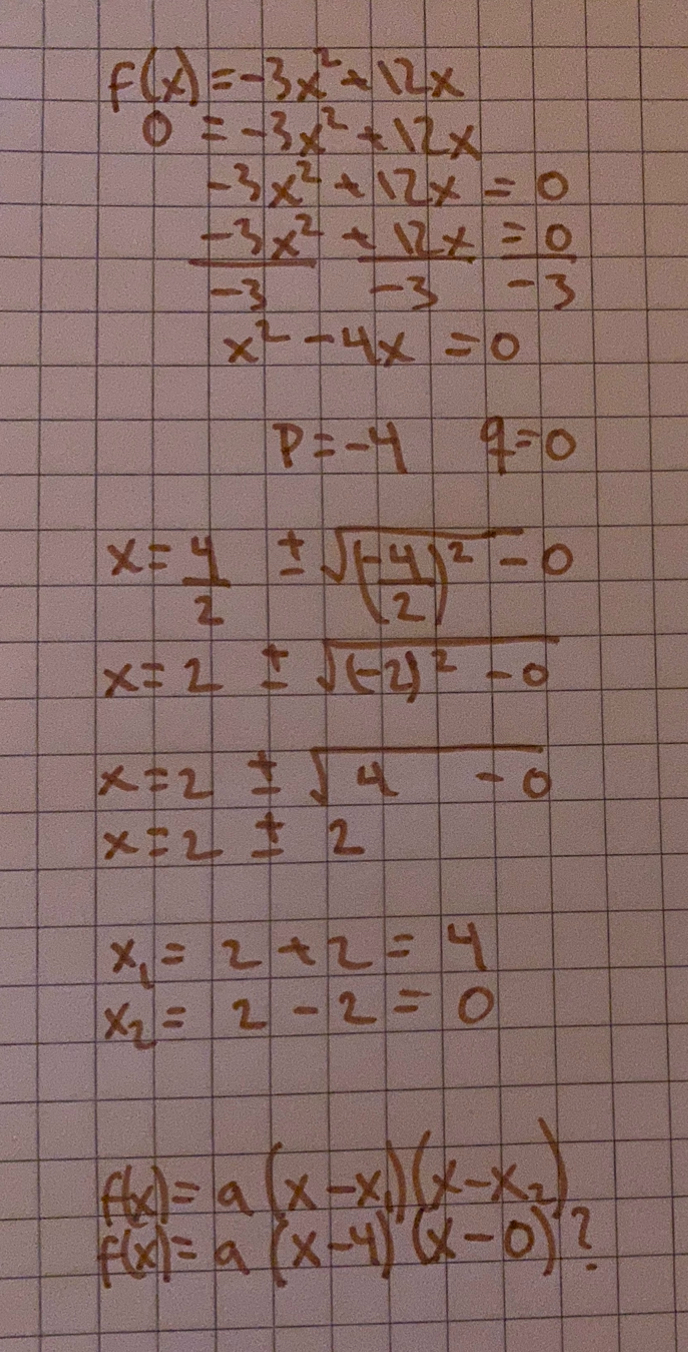Blir nollvärdet på x-axeln: x=4 & x=0 ? 
& om det är så, hur får jag reda på 3e punkten utifrån denna info? 

Ja, rötterna till f(x) är 0 och 4.

Du behöver ingen specifik 3e punkt. Ta bara någon punkt p mellan 0 och 4 och räkna ut f(p).

Man behöver inte räkna alls. Om koefficienten för x² i en andragradsfunktion är negativ så finns det ett maximum ("ledsen mun").

Jag gjorde så här..

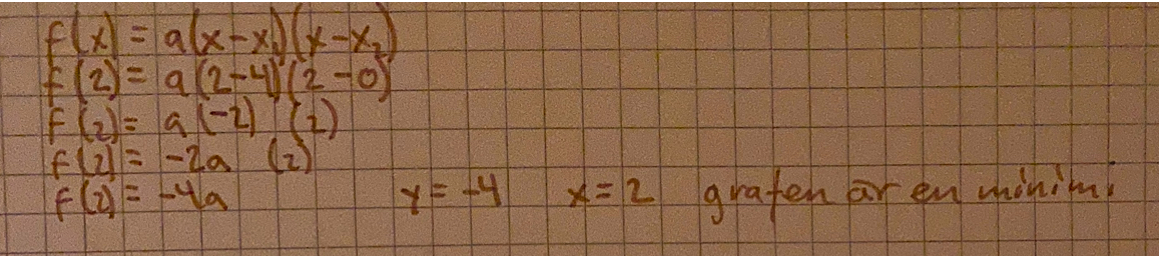om jag tar en x koordinat som är 2 & sätter in & försöker räkna fram ett y värde får jag då typ att det blir y= -4 & -a är ledsen mun maximi (står minimi på pappret de är fel mena maximi). 

så kan jag säga att funktionen

f(x)= -3x^2 + 12 x 

har en maximipunkt & att den punkten har koordinaten  

y=-4 x=2 

är de rätt tänkt /gjort då? 

om f(2)=-4 hade det varit en minimipunkt, eftersom att f(0)=f(4)=0.

Du råkar byta tecken när du räknar du det, så det ska bli f(2)=4, vilket är en maximi

okej, så när jag får fram f(2)=-4a i min uträkning så är det alltså att y = 4  så jag får bara tänka lite tvärtom ?

** För jag förstår inte hur jag i uträkningen kan då fram 4, de blir ju liksom -4 där.  

Alltså egentligen behöver du hitta en tredje punkt för att bestämma a.

Men du vet redan att a är negativt. Testa att expandera det funktionsuttryck du får och jämför med usprungsfunktionen.

Som Laguna skrev i #11: Du behöver inte räkna alls. Om koefficienten för andragradstermen är positiv ser kurvan ut så här: U. Om koefficienten för andragradstermen är negativ ser kurvan ut så här: $\cap$.

Ja, men eftersom att b) uppgiften är:
Bestäm koordinaterna (x,y)för maximum eller minimum punkten.
Så har jag inte så mycket mer att gå på än de jag har så därför tänkte jag att jag kan skriva den punkten?

Andragradsfunktioner kommer alltid vara symmetriska. Symmetrilinjen (den linje som skär extrempunkten) är mellan de 2 rötterna.

Naturens skrev:

Ja, men eftersom att b) uppgiften är:
Bestäm koordinaterna (x,y)för maximum eller minimum punkten.
Så har jag inte så mycket mer att gå på än de jag har så därför tänkte jag att jag kan skriva den punkten?

Om b-uppgiften är så, är det vettigt att ta fram de båda nollställena, men det är inget vi kan gissa av att läsa ditt förstainlägg. 

Du behöver inte hitta nollställena för att bestämma symmetrilinjen.

Som jag skrev i det här svaret:

Om funktionen är skriven på standardform f(x) = ax²+bx+c så ligger symmetrilinjen vid x = -b/(2a).

I det här fallet är a = -3, b = 12 och c = 0, vilket direkt ger symmetrilinjen x = -12/(2*(-3)), dvs x = 2.

Eftersom extrempunkten ligger på symmetrilinjen så fås y-koordinaten ur f(-b/(2a)), dvs y = f(2) i det här fallet.

För den som är intresserad:

Ur formelbladets beskrivning av pq-formeln och lösningsformeln ("abc-formeln") framgår det var symmetrilinjen ligger (gulmarkerat).och att denna ligger mitt emellan eventuella reella nollställen;

okej, tack.. får nog läsa de där ett par gånger & öva på för att få in..
Fick fram x värdet dvs 2, tänkte bara mitten av nollställena så liksom fick jag x=2 då nollställena är x=0 och x=4. 
Men om jag ska ge koordinaten för maximipunktens y värde så måste de ju vara rätt att jag stoppar in alla värden jag har dvs nollställena samt x värdet 2 (x värde för extrempunkten) i formen f(x)=a(x-x1)(x-x2) för att vidare få fram ett a värde som då blir y värdet (för extrempunkten): 
f(x)=a(x-x1)(x-x2).   som blir f(2)=a(2-4)(2-0)  får då att f(2)=-4a  som då jag tolkar som att y= -4 om x=2 ?

***
Tänker att de är de enklaste sättet för mig att få fram ett korrekt y värde för de x värdet just i denna uppgift. Där jag nu har en del info jag kan använda mig av ?
 

Vilket som är det enkaste sättet FÖR DIG kan ingen annan än du veta.

Två modeller du kan undersöka, för att kolla vilken som är enklast ör dig:

1) f(x)=-3x²+12x = -3(x²-4x) = -3x(x-4) så symmetrilinjen är mittemellan nollställena ,d v s x = 2.

2) f(x)=-3x²+12x = -3(x²-4x), använd pq-formeln "till hälften" och se att symmetrilinjen är x = -(-4/2) = 2.

Det finns säkert ännu fler sätt att resonera.

Okej, tack för all hjälp