Från ekvation till en grafisk lösning (andragradsekvation)
Hej,
Jag kollar gamla uppgifter från tidigare kapitel som kanske kan hjälpa mig "komma ihåg" hur jag kan lösa denna uppgift.
Uppgiften är: Lös ekvationen x^2-2x-8=0 grafiskt
Min tanke till lösning:
1) Ekvationen x^2-2x-8=0 kan jag använda PQ formeln på.
2)Kan med hjälp av PQ få fram 2 st X värden, detta med hjälp av att räkna fram de två x värden med pq.
Grafiskt kan jag sen:
3) Ta de två x värden och placera in dom i ett koordinatsystem dvs två punkter på x-axeln som funktionen "går igenom". Dessa x värden blir då funktionens två nollställen.
Men jag vet ju inte så mycket mer! Exempel minimipunkt eller maximipunkt? Vet inte om den ska skära y axeln något heller. Jag vet inte hur funktionen ska se ut mer än att den ska gå igenom de två nollställena, så vet inte riktigt hur jag ska tänka för att få fram mer information om funktionen?
Naturens skrev:Hej,
Jag kollar gamla uppgifter från tidigare kapitel som kanske kan hjälpa mig "komma ihåg" hur jag kan lösa denna uppgift.
Uppgiften är: Lös ekvationen x^2-2x-8=0 grafiskt
Min tanke till lösning:
1) Ekvationen x^2-2x-8=0 kan jag använda PQ formeln på.
2)Kan med hjälp av PQ få fram 2 st X värden, detta med hjälp av att räkna fram de två x värden med pq.
Grafiskt kan jag sen:
3) Ta de två x värden och placera in dom i ett koordinatsystem dvs två punkter på x-axeln som funktionen "går igenom". Dessa x värden blir då funktionens två nollställen.
Men jag vet ju inte så mycket mer! Exempel minimipunkt eller maximipunkt? Vet inte om den ska skära y axeln något heller. Jag vet inte hur funktionen ska se ut mer än att den ska gå igenom de två nollställena, så vet inte riktigt hur jag ska tänka för att få fram mer information om funktionen?
Att lösa en ekvation grafiskt betyder att man ritar upp VL och HL i samma koordinatsystem och undersöker var de båda kurvorna skär varandra.
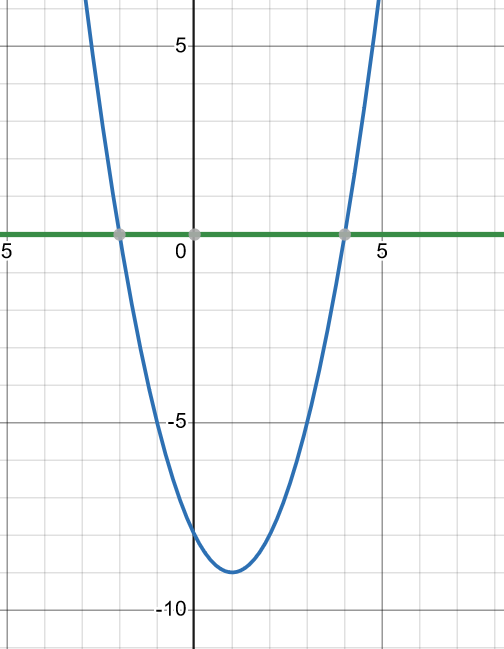
Tack för svaret.
Så.. menar du då, att jag:
1) tar: x^2-2x-8=0
2) VL: x^2-2x-8
3) HL: 0
4) jag räknar fram vart skärningspunkten ska vara på x^2-2x-8 med hjälp av pq
5) jag tar det två x värden jag räknat fram från x^2-2x-8 med hjälp av pq och placerar in de i ett koordinatsystem
6) jag tar sen H.L som är =0
7) och placerar in 0 i samma koordinatsystem (dvs på x-axeln)
8) och se vart de båda kurvorna skär sig? vad menas här? Visst kan jag skissa en kurva från ena x stället till den andra, vet dock inte "hur djupt ner eller upp" den kurvan ska vara, men kan skissa en kurva från ena x stället till de andra. Men på punkten 0 så kan jag ju inte skissa någon kurva det finns ju bara en punkt?
***
Lägger till: Och om punkten 0 placeras då är det ju origo och om jag ska försöka få x ställernas kurva att "möta" 0 då kan det ju gå hur djupt "ner" eller "upp" som möjligt?
Nej, om du räknar så löser du inte ekvationen grafiskt. Du skall bara titta på bilden som jag la upp.
Förlåt men jag förstår inte. Jag ser bilden du gjorde. Men hur vet du vart du ska placera ut nollställena då? du måste ju ha räknat fram det på något vis?
***
Om jag ska lösa ekvationen grafiskt så måste jag väl förstå vad ekvationen visar så jag kan "ta in" ekvationen till ett koordinatsystem för att då "omvandla" ekvationen till en graf liksom?
Nej, jag la bara in funktionen i Desmos. Det programmet ritar upp funktionen automatiskt.
När man ritar upp en funktion för hand gör man så här:
*Välj ett värde på x. Beräkna motsvarande y-värde. Markera punkten (x,y) i koordinatsystemet. Upprepa från * tills du kan se hur funktionen ser ut.
När jag gick på gymnasiet fanns det inga grafräknare, utan vi behövde räkna ut alla y-värden och pricka in punkterna för hand.
Pricka in för hand!!! ..oj.. okej..
Men liksom om jag har denna ekvation: x^2-2x-8=0 och inte gör något med den, dvs inte räknar fram x1 & x2.
Då betyder ekvationen att V.L (x^2-2x-8) = H.L (0). Och då betyder väl "Lös ekvationen grafiskt",
att där parabeln skär x axeln där är lösningen till uppgiften, för de är där kurvan x^2-2x-8 ÄR = 0
Har jag förstått det rätt? Om om så:
Hur kan man "se" hur kurvan/parabeln ska se ut bara genom att se: x^2-2x-8.
På K-form är de ju enkelt, dvs y=Kx+m för då ser jag att k är lutningen och m är skärningen med y axeln & så är det bara att skissa, men när man bara har: x^2-2x-8 så blir det svårare ju... Jag vet att x^2 betyder andragrad så en parabel, men resten då? ...För om jag inte får räkna fram x värden så blir de ju för mig att "se" hur kurvan ska se ut genom att se och förstå kurvan genom bara: x^2-2x-8
Är det så att lutningen är -2 och skärningen med y axeln är -8 ? (gissar bara nu utifrån k-form)
Om jag då ska välja ett värde på x? då väljer jag -2x som det står i ekvationen.
Om jag ska beräkna motsvarande y värde, så om x=-2 där är ju y=0,
Punkten på koordinatsystemet blir då -2,0
och det sista förstår jag inte, för alla x värden jag ger ut kommer ju ha ett y värde som är 0..
Jag vill bara veta hur jag "ser" hur kurvan ska se ut genom att bara se : x^2-2x-8
Vänta lite nu... Vänta... lite... nu... de ser ju ut som de på din bild..
Alltså...
Att x^2-2x-8 ÄR:
x^2 betyder att de är en andragradare så en parabel dvs 2st ställen parabeln skär x-axeln och därmed 2 lösningar!
-2x är lutningen så parabeln går ner
och -8 är skärningen med y axeln!
och det är då bara att skissa upp den och sedan se vart parabeln "träffar" 0 och där är lösningarna!
eller hur?
Om du börjar med att lösa ekvationen finns det ingen anledning att rita upp den. Meningen med den här uppgiften är att du skall lösa ekvtionen grafiskt, inte på något annat sätt.
jag hänger med på vad jag ska göra, tror jag. Tack


