Fråga på en uppgift

Min fråga är har alla rätvinkliga trianglar i ett koordinatsystem en lutning på deras bas / höjd som är -1 ?

Nej, däremot gäller det för två linjer som är vinkelräta mot varandra att produkten av deras k-värden är lika med -1.

Kan du ladda upp en bild av uppgiften och din lösning så hjälper vi dig vidare?

Tack för svaret. Okej.

Uppgiften är: Punkterna (1,1) (6,6) (4,-2) bildar en triangel.
Undersök om triangeln är rätvinklig. (det finns ingen bild) 

Jag fick fel på uppgiften. för mitt svar bara ett "Ja", jag skulle räkna fram mig till svaret dvs ett -1 och de skulle då på något vis betyda att triangeln är rätvinklig. Så.. det förvirra mig något..  

***
Förklaringen jag fick var detta:

Räkna fram lutningen för linjen AB och AC

AB= (1,1)(4-2) lutningen är K1 (2-1) / (4-1) = -3/3 = -1
AC= (1,1)(6,6) lutningen är K2 (6-1) / (6-1) = 5/5 = 1

k1*k2= -1*1= -1 triangeln är rätvinklig 

Så det förvirra mig något, jag missuppfatta uppgiften helt, och inte nog med det så ska jag räkna någon lutning som vidare ska ge mig ett svar som då ska få mig att förstå att triangeln är rät, det är typ super komplicerat!

Börja med att rita upp triangeln och lägg upp bilden här. Förhoppningsvis syns det vilken vinkel som skulle kunna vara rät, så då behöver vi inte räkna ut alla riktningskoefficienterna utan "bara" två.

Naturens skrev:

Tack för svaret. Okej.

Uppgiften är: Punkterna (1,1) (6,6) (4,-2) bildar en triangel.
Undersök om triangeln är rätvinklig. (det finns ingen bild) 

Jag fick fel på uppgiften. för mitt svar bara ett "Ja", jag skulle räkna fram mig till svaret dvs ett -1 och de skulle då på något vis betyda att triangeln är rätvinklig. Så.. det förvirra mig något..  

Om frågeställningen är som du skriver så måste svaret vara "Ja" eller "Nej".

Svaret kan då varken vara "-1" eller något annat numeriskt värde. 

Däremot är vördet -1 relevant i uträkningarna som lugger till grund för svaret, se tidigare svar.

Kan du ladda upp en bild på själva uppgiften och på facit?

Naturens skrev:

[...]
Så det förvirra mig något, jag missuppfatta uppgiften helt, och inte nog med det så ska jag räkna någon lutning som vidare ska ge mig ett svar som då ska få mig att förstå att triangeln är rät, det är typ super komplicerat!

• En triangel består av tre sidor.
• Varje sida har en viss lutning.
• Om två sidor är vinkelräta mot varandra så är triangeln rätvinklig, annars inte.

En rättfram metod att bestämma huruvida triangeln är rätvinklig eller inte är då att

1. beräkna de tre lutningarna med hjälp av $k=\frac{\Delta y}{\Delta x}$
2. parvis multiplicera lutningarna med varandra
3. kontrollera om någon av de tre produkterna är kika med -1

Säg till om något i detta är oklart, så ska vi försöka förklara mer ingående.

=====

"Felet" du gjorde var antagligen att du bara svarade Ja utan att visa hur du kom fram till det.

Du skulle också kunna räkna ut längden av alla tre sidorna och undersöka om Pythagoras sats stämmer för triangeln - om den stämmer är triangeln rätvinklig, annars inte.

Smaragdalena skrev:

Du skulle också kunna räkna ut längden av alla tre sidorna och undersöka om Pythagoras sats stämmer för triangeln - om den stämmer är triangeln rätvinklig, annars inte.

Det stämmer, men det är mer komplicerat att beräkna sidlängderna än att bestämma lutningarna.

Okej här kommer en bild:

***
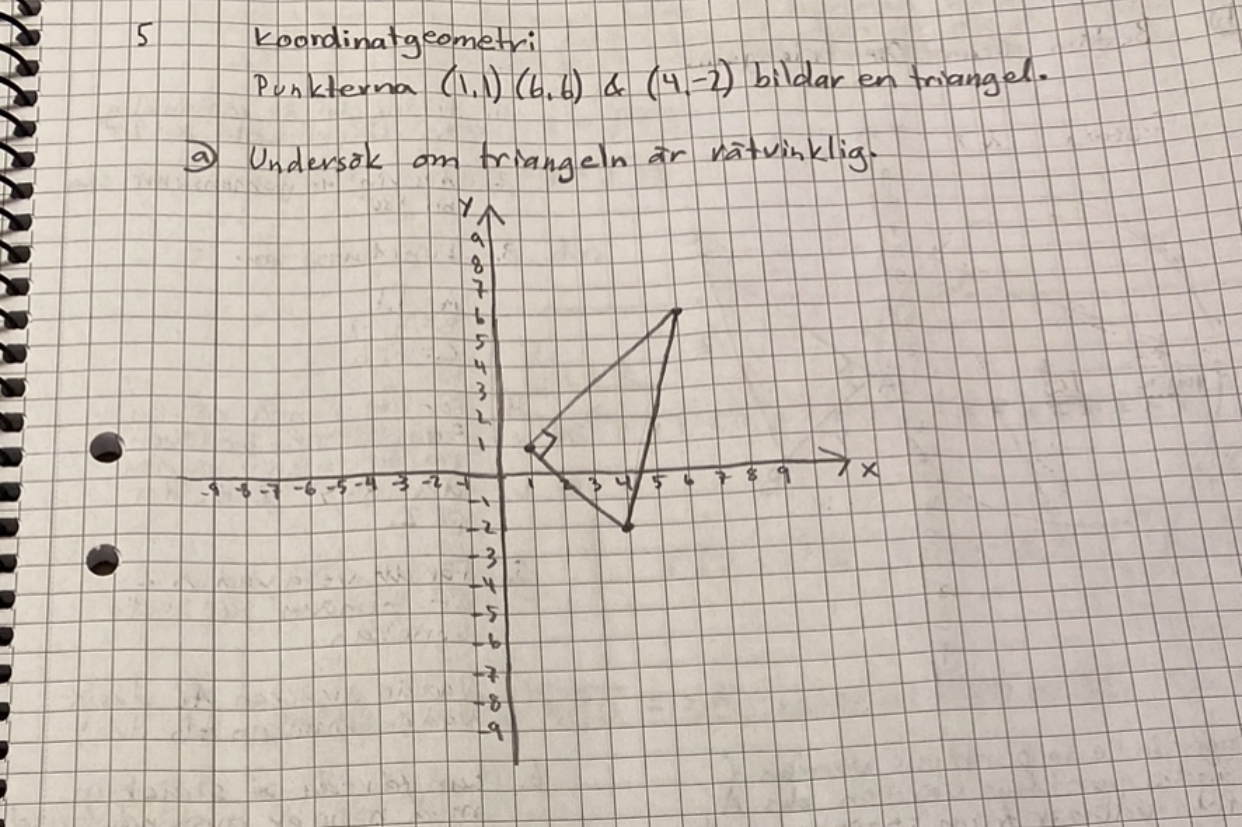
Okej tack. Jag får skriva upp de vid uppgiften och räkna om det. 

Smaragdalena skrev:

Du skulle också kunna räkna ut längden av alla tre sidorna och undersöka om Pythagoras sats stämmer för triangeln - om den stämmer är triangeln rätvinklig, annars inte.

Yngve skrev:

Det stämmer, men det är mer komplicerat att beräkna sidlängderna än att bestämma lutningarna.

Det stämmer också det Yngve skriver. Å andra sidan har du redan beräknat två av sidlängderna i b), detta i din förra tråd för denna uppgift. Så på ett sätt blir det mer enhetligt att bara hålla sig till Pythagoras.

Tack