Fråga gällande uträkning av komplexa rötter
Uppgiften är: 8x^2 = -98
Försökte lösa uppgiften genom att räkna bort 8an i v.l (sen även h.l) först men det vart fel. Hitta en lösning som jag följde och fick rätt enligt facit, men förstår inte hur de kommer sig att jag kunde använda mig av en 2:a när det inte finns en sådan i ekvationen? När får man använda sig av andra siffror än det som följer med ekvationen & när ska man veta att man ska göra det?
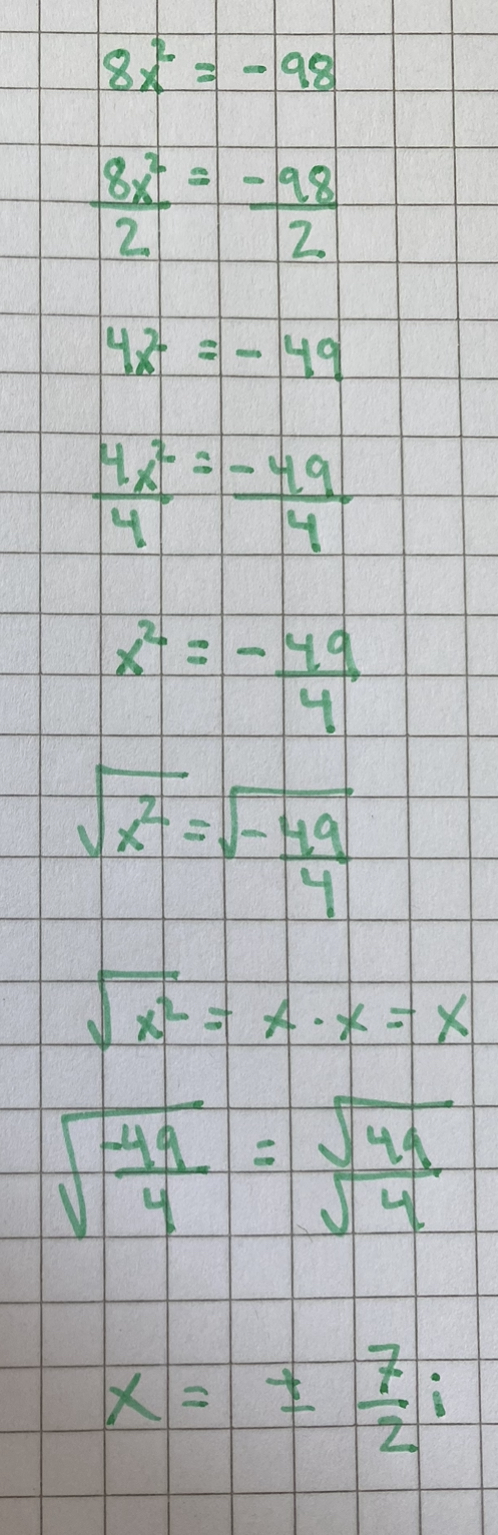
Ifall du menar divisionen med 2 på din andra rad, så är svaret att
Om man gör samma sak med högerledet som med vänsterledet, så gäller fortfarande ekvationen.
Man kunde lika gärna dela med 12 eller 739, ekvationen fortsätter gälla i alla fall.
Roten ur x2 måste inte vara x. Roten ur (-3)2 är inte-3 utan 3.
Så jag kan dividera (eller multiplicera?) med tal som inte finns i ekvationen, så länge jag gör samma i båda leden
Ja, du kan i stort sett göra vad som helst med en en ekvation bara du gör samma sak på båda sidor!
Detta beror på att de två sidorna är lika, och om du du gör samma sak på båda sidorna så förblir de lika!
(Det finns naturligtvis en del fällor man kan kliva i, om man t.ex delar med något som är 0 blir det tok, och om man kvadrerar så kan man få falska rötter som man måste hålla koll på)
Tack. Men fråga, vad menar du med att om man delar något med 0? Jag har gjort de på två uppgifter och fått rätt på båda?
Naturens skrev:Tack. Men fråga, vad menar du med att om man delar något med 0? Jag har gjort de på två uppgifter och fått rätt på båda?
Att dela ett tal med 0 är odefinierat, det går inte.
tack


