Fråga gällande i
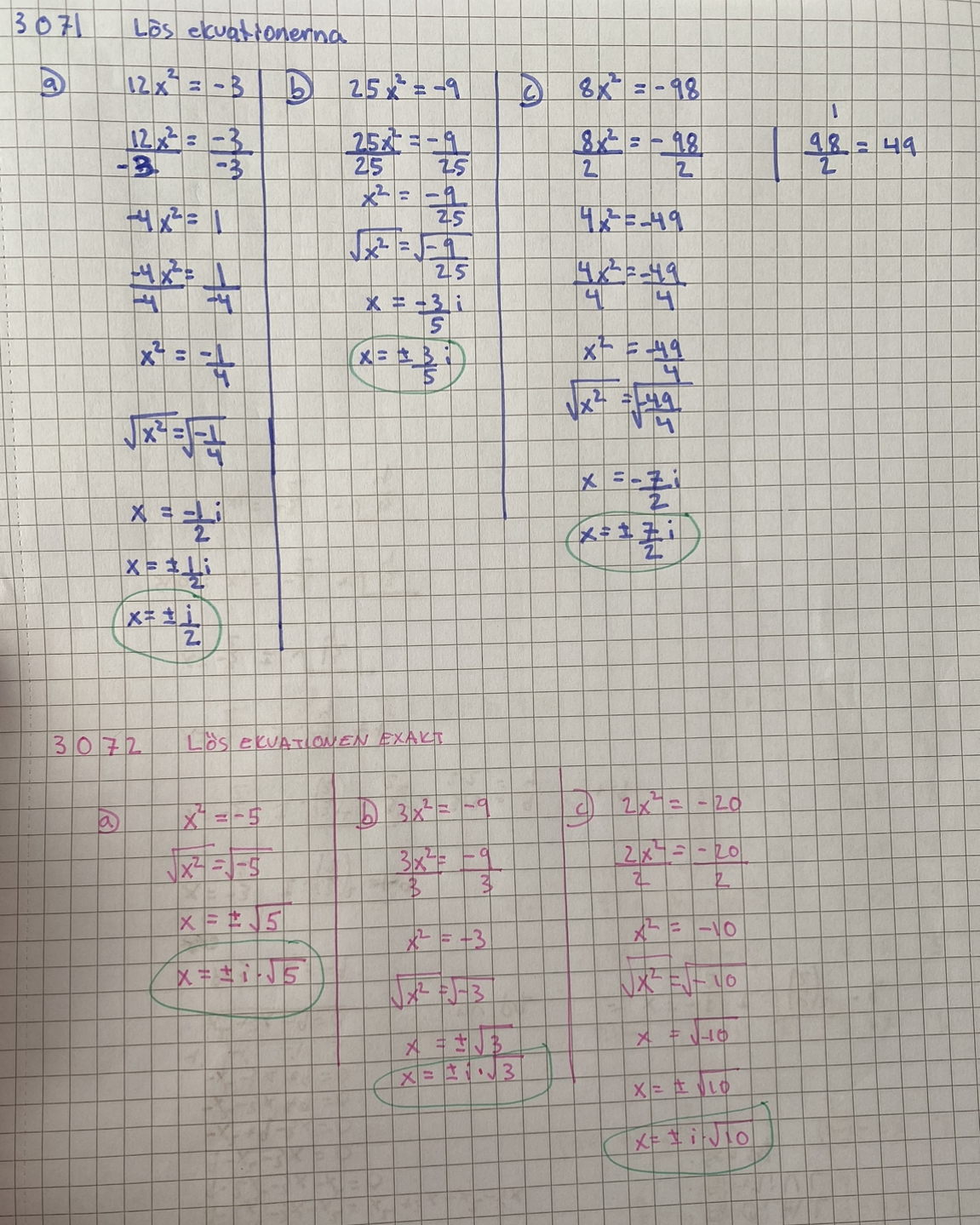 vad är skillnaden med att ha i bakom siffran som i de blå uppgifterna / framför rottecknet som i de rosa uppgifterna. Det jag egentligen ville svara med i rosa var x = +/- roten ur sen den siffran. Men facit säger att man ska svara x= +/- i roten ur sen siffran. Vad menas de svaret? Jag förstår vad det blåa betyder exempelvis 7/2i = 7/2 gånger i dvs 7/2 * -1. Men svaret till rosa vet jag inte riktigt vad som menas, även fast jag kan typ räkna fram det.
vad är skillnaden med att ha i bakom siffran som i de blå uppgifterna / framför rottecknet som i de rosa uppgifterna. Det jag egentligen ville svara med i rosa var x = +/- roten ur sen den siffran. Men facit säger att man ska svara x= +/- i roten ur sen siffran. Vad menas de svaret? Jag förstår vad det blåa betyder exempelvis 7/2i = 7/2 gånger i dvs 7/2 * -1. Men svaret till rosa vet jag inte riktigt vad som menas, även fast jag kan typ räkna fram det.
Ingen skillnad alls, båda sätten betyder multiplikation.
, men man brukar aldrig sätta en siffra sist, det kan missförstås som i3 eller i3.
, och här är det man kan råka blanda ihop det med.
Tack för svaret. Men sen så undrar jag om i (roten ur) 10 är -1 * (roten ur) 10. Men -1 * (roten ur) 10, går ju inte? så då kan man ju inte ta -1 * (roten ur) 10?
Om du undrar ifall är lika med så är svaret nej.
Om det vore sant så skulle det innebära att , vilket inte är fallet.
Däremot gäller det att eftersom och att vi då får
======
Men visst kan man beräkna .
På samma sätt som t.ex. så är vilket är ungefär lika med , eftersom .



