Fråga gällande geometri

Kan du lägga upp en bild på uppgiften, eller rita upp trianglarna själv? Jag har lite svårt att följa med i ditt resonemang. 

Hej, tack för svaret. 

här kommer en bild på uppgiften.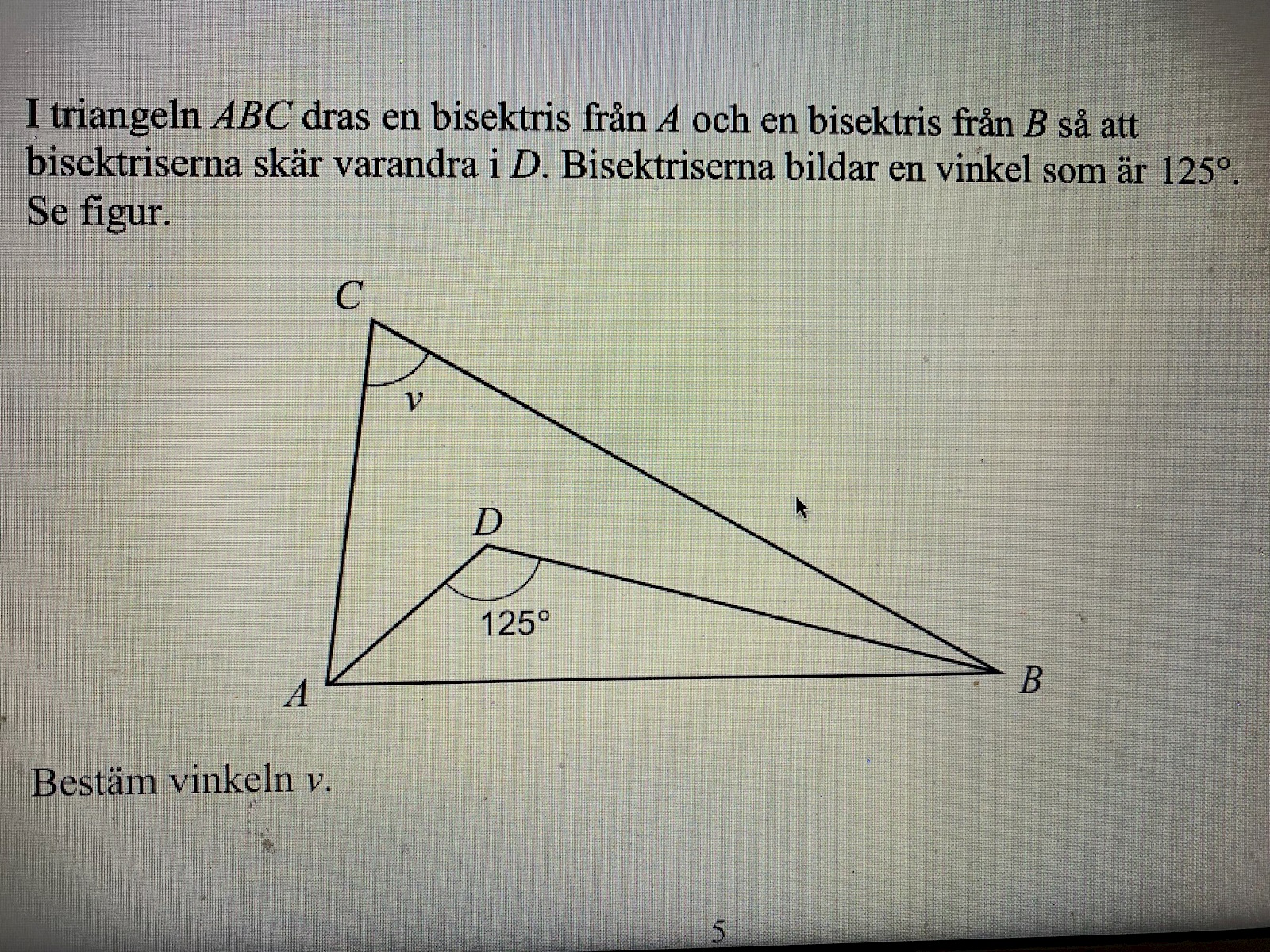 

Har sett en genomgång på denna uppgift, och i den genomgången så sa han att man gör två ekvationer. 

Den lilla triangelns hörn blir kallade x & y. Hörnen bredvid lilla triangelns hörn x & y. Blir då också kallade x & y. 

om x+y+125 = 180 och detta blir x+y= 55

då tänker jag så här. Att om den stora triangelns hörn är 2x ihop & 2y ihop samt vinkel v. Borde man då inte sätta ihop hörnet från den lilla dvs 55 + hörnet från den andra”stora” som då är 55 & det ihop blir vad den stora triangeln har. 

ekvationen han visa för den större triangeln var 2x+ 2y+v=180 och 2x är ju 2 gånger x & här blir jag något förvirrad? & om x & y är 55 dvs x+y+125=180 blir 55+55+125=180 borde då 2x+2y+v=180 inte blir 2gånger x ? Men den ”lilla” triangelns vinklar är 55 för att vinkelsumman ska bli 180. Och det är en bisektris så tänker jag om en bisektris delar vinklarna i lika stora delar så borde ”den andra delen” vara 55 MED. Och ihop blir de då 110. Dvs triangel ABC vinklar blir väl då 55+55=110 för att bisektrisen delar vinklarna i lika stora delar? Triangeln ABC blir inte 55 som han skrev i sin uträkning med 55+55+v=180? Och om det är så att triangeln ABCs vinklar är 55*55 varför är ekvationen 2x+2y och inte bara x+y+v=180 då denna förklarar triangeln ABC bättre? 

**
Vet inte om jag förklarar min fråga eller tanke bra. Men frågan är, en bisektris delar ju vinkeln i lika stora delar. Om den ena delen är 55 borde den andra då också vara 55. ihop blir då "den vinkeln" utan bisektrisen 110. Ekvationen läraren visa som representera den stora triangeln var 2x+2y+v=180, men 2x är ju 2*x och 2*x blir ju då 2*55 och här blir de ju inte att den vinkeln blir 55 som det ska vara, utan här blir vinkeln större.

Det stämmer att vinklarna (inte hörnen) x och y uppfyller sambandet x+y+125° = 180°, dvs x+y = 55°.

Du vet även att 2x+2y+v = 180°, se bild.

Detta kan skrivas 2(x+y)+v = 180°.

Kommer du vidare då?

men jag tänker så här. 
Om triangel ABDs x vinkel är 55, då borde triangeln ABCs x vinkel vara 55+55 dvs 110 och inte bara 55. Förstår inte hur vinkeln x i ABC kan ses som lika stor som vinkeln x i ABD. Det är ju 2 x vinklar och de borde då bli en större vinkel tänker jag. 

**
och inte gånger för de blir ju för mycket dvs inte 2x för de skulle ju bli 2 gånger 55, utan tänker mig + dvs 55+55 och då undrar jag hur uttrycket 2x+2y+v=180 kan liksom stämma?

Naturens skrev:

men jag tänker så här. 
Om triangel ABDs x vinkel är 55, då borde triangeln ABCs x vinkel vara 55+55 dvs 110 och inte bara 55.

Men vinkel x är inte 55°. Det är summan av x och y som är 55°, dvs x+y = 55°

Förstår inte hur vinkeln x i ABC kan ses som lika stor som vinkeln x i ABD. Det är ju 2 x vinklar och de borde då bli en större vinkel tänker jag. 

Det står i uppgiften att det i triangeln ABC dras en bisektris från A till D. Det betyder att sträckan AD delar vinkeln $\angle$CAB i två lika stora delar, nämligen $\angle$CAD och $\angle$DAB. Om vi kallar den ena delen x så måste även den andra delen vara x. Vinkeln vid A i triangeln ABD (dvs $\angle$DAB) är x och vinkeln vid A i triangeln ABC (dvs $\angle$CAB) är 2x.

**
och inte gånger för de blir ju för mycket dvs inte 2x för de skulle ju bli 2 gånger 55, utan tänker mig + dvs 55+55 och då undrar jag hur uttrycket 2x+2y+v=180 kan liksom stämma?

Se bilden i svar #4. Är du med på att $\angle$CAB = 2x och att $\angle$ABC = 2y?

Jag förstår att $\angle CAB=2 st X och att \angle ABC=2 st y$

Men jag förstår inte hur:

 $$\begin{gathered} \angle CAB=2·x eller hur \angle ABC=2·y \\ som jag tolkar att detta betyder: \\ \angle CAB=2x samt \angle ABC=2y dvs gånger mellan 2 och variabel \end{gathered}$$