Fråga gällande Gausselimination
Jag har egentligen bara en fråga.
Jag har ekvationerna/ ekvationssystemet:
2x+y+z=95
y+z=40
x+2y=55
Jag skulle vilja lösa detta system med hjälp av trappsystemet, men eftersom att två av ekvationerna endast innehåller två obekanta och inte tre så blir de ju svårt att använda trappsystemet. Så de jag gjorde var att jag la in den obekanta som "fattades" i den ekvationen alltså:
2x+y+z=95 (la inte till något den är 3)
x+y+z=40 (la till +x)
x+2y+z=55 (la till +z)
Ville väl egentligen bara experimentera för att se, om jag skulle kunna få fram värdet på X då det är vad textuppgiften vill få fram (eller textuppgiften pratar om jordgubbar/potatis/morötter och vill veta vad jordgubbar kostar, men jag gjorde som så att jag gav X= jordgubbar, Y = potatis och Z = morötter och gjorde ett system).
Jag kommer väldigt nära den summan som jordgubbar kostar, men inte riktigt hela vägen fram, alltså de blir inte riktigt rätt. Undrar om de är för att JAG räknat fel eller om de är för att man INTE får/kan göra så som jag tänker.
Boken har en förklaring på hur man gör, men den är jätte förvirrande och konstig. Tycker trappan är bra, så vill testa den även här. Får ju ut rätt svar annars när jag har tre obekanta i ett ekvationssystem på tre. Men just här blir de ett ekvationssystem på tre ekvationer där bara 1 innehåller tre obekanta och resten 2, så de blir liksom, svårare för mig att använda trappan, om de ens går?
vet inte om jag förklarar de där bra, men hoppas det.
Elgib skrev:2x+y+z=95 (la inte till något den är 3)
x+y+z=40 (la till +x)
x+2y+z=55 (la till +z)
Undrar om de är för att JAG räknat fel eller om de är för att man INTE får/kan göra så som jag tänker.
Jag vet inte om du har räknat fel eller inte eftersom du inte visar hur du har räknat, men det är helt säkert att du INTE får göra som du har gjort, nämligen att lägga till x i en ekvation och z i en annan.
Då betyder ju ekvationerna något helt annat än vad de gjorde från början.
Se här:
Om x, y och z betyder det du har beskrivit ovan så är ju den ursprungliga lydelsen av ekvation 2:
"1 enhet potatis plus 1 enhet morötter kostar 40"
Men efter att du har lagt till x lyder ekvationen:
"1 enhet jordgubbar plus en enhet potatis plus 1 enhet morötter kostar 40".
Ser du att det är en helt annorlunda mening?
======
Jag är lite osäker på vad du menar med "trappsystemet". Kan du visa ett exempel?
Jo, de låter logiskt, men tack då vet jag säkert.
här kommer en bild på trappsystemet
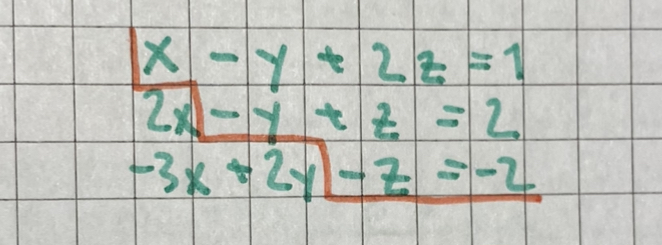
****

OK. Gör då så att du helt enkelt subtraherar ekvation 2 från ekvation 1, vilket ger dig 2x = 55.
Du kan då skriva detta tillsammans med ekvation 3 på "trappform":
2y+x = 55
2x = 55
x och z saknas inte, det är bara att det står 0x och 0z. Du kan göra gausselimination på det ursprungliga systemet, du får bara räkna med att det står nollor på vissa platser


