Fråga gällande Formen f(x) = ax2 + bx + c

Förstår att de är konstanter men var ligger a:et och b:et på linjen, dvs c är ju skärningen med y-axeln så kan jag då se vad a:et och b:et är /ligger i en graf bara genom att titta på grafen/linjen?

Det korta svaret är att det inte bara går att "se" vilka värden $a$ och $b$ har. Men jag förstår inte vad du pratar om för "linje"?

För att se hur konstanterna a och b påverkar utseendet på en andragradare kan du använda Geogebra.

1, Skapa två sliders (a, b och c) genom att klicka a -> Enter, b -> Enter och c -> Enter.

2, Skriv in funktionen ax²+bx+c

Färdigt! Varsågod att leka runt lite.

Eller använda Desmos. Desmos är bättre för 2D-grafer. GeoGebra är krångligt och mindre stilrent.

Krångligt är det väl ändå inte att genomföra det ovannämnda?

Naturens skrev:

Hej,

Ska lära mig att lösa funktioner på formen f(x) = ax2 + bx + c. Har försökt hitta någon förklaring som förklarar enkelt vad a:et och b:et betyder, alltså vad de är i linjen, men hittar inget som förklarar bra. Vet att C är där linjen eller grafen skär y-axeln, men vad representerar a och b på linjen eller grafen? Förstår att de är konstanter men var ligger a:et och b:et på linjen, dvs c är ju skärningen med y-axeln så kan jag då se vad a:et och b:et är /ligger i en graf bara genom att titta på grafen/linjen?

Du kan skriva

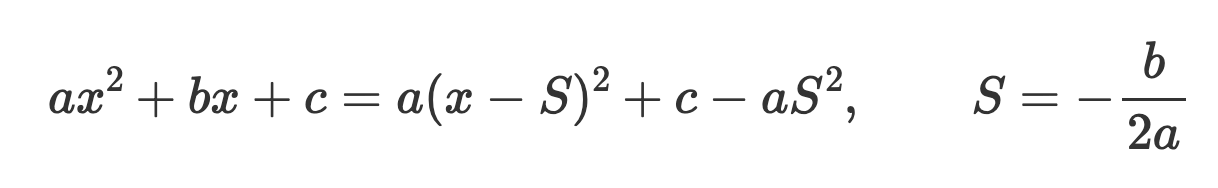
vilket ger att symmetrilinjen är x=S och vertex är (S,c-aS^2) samt skärning med x-axeln för

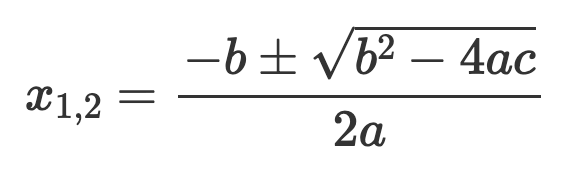
Jag vet inte om det är detta du menar med "linje".

Med linje menar jag parabelns utseende. Man ser vart parabeln skär y axeln och undra om a och b var lika "enkelt" att liksom se var de värden är. Men som jag förstår det här så går det inte att se. Utan antar att de bara går att få ut de värdet genom uträkning. 

Hitta en sida som säger att

"Konstanten b förflyttar grafen i både sid och höjdled samtidigt." vilket jag antar betyder att y värdet då också kan ändras..? och sidled antar jag dom menar på x-axeln. 

"Konstanten a påverkar parabelns utseende genom att stora negativa värden på a resultera i en smal och negativ graf, till att bli bredare och bredare ju närmre värdet noll a kommer". 
Kanske ska se de program ni rekommendera här för att få en bild på hur de här kan se ut.

Du kanske menar kurva när du säger linje. En linje är rak.

Ja precis kurva, sorry!

Mrpotatohead skrev:

Krångligt är det väl ändå inte att genomföra det ovannämnda?

Nej men GeoGebra som verktyg är generellt krångligare. Dessutom suger det verktyget upp ALLA CPUns resurser. Så fort jag öppnar GeoGebra så skjuter min CPU iväg till typ 50 % usage.

Naturens skrev:

Med linje menar jag parabelns utseende. Man ser vart parabeln skär y axeln och undra om a och b var lika "enkelt" att liksom se var de värden är. Men som jag förstår det här så går det inte att se. Utan antar att de bara går att få ut de värdet genom uträkning. 

Hitta en sida som säger att

"Konstanten b förflyttar grafen i både sid och höjdled samtidigt." vilket jag antar betyder att y värdet då också kan ändras..? och sidled antar jag dom menar på x-axeln. 

"Konstanten a påverkar parabelns utseende genom att stora negativa värden på a resultera i en smal och negativ graf, till att bli bredare och bredare ju närmre värdet noll a kommer". 
Kanske ska se de program ni rekommendera här för att få en bild på hur de här kan se ut.

Ja, vi förstod vad du menade. Om du vill se svaret till din fråga visuellt och grafiskt så föreslår jag återigen Geogebra, eller Desmos. 

naytte skrev:

Mrpotatohead skrev:

Krångligt är det väl ändå inte att genomföra det ovannämnda?

Nej men GeoGebra som verktyg är generellt krångligare. Dessutom suger det verktyget upp ALLA CPUns resurser. Så fort jag öppnar GeoGebra så skjuter min CPU iväg till typ 50 % usage.

Föredrar oxå Desmos. Visste ej det om CPU-grejorna.

För det lilla Naturens dock ska göra så kvittar vilket verktyg väljer.