Fråga 38: z=bi-5
Jag förstår inte varför jag får -2.4, jag hänger med på att det kommer från -5 men vad är det jag gör fel som gör att det blir negativt?
Dessutom hänger jag inte med på formlen tanv=b/a. Det kan väl vara a/b också om figuren är i andra kvadranten? Finns någon någon sorts härledning till formeln online, YouTube video eller någon artikel?

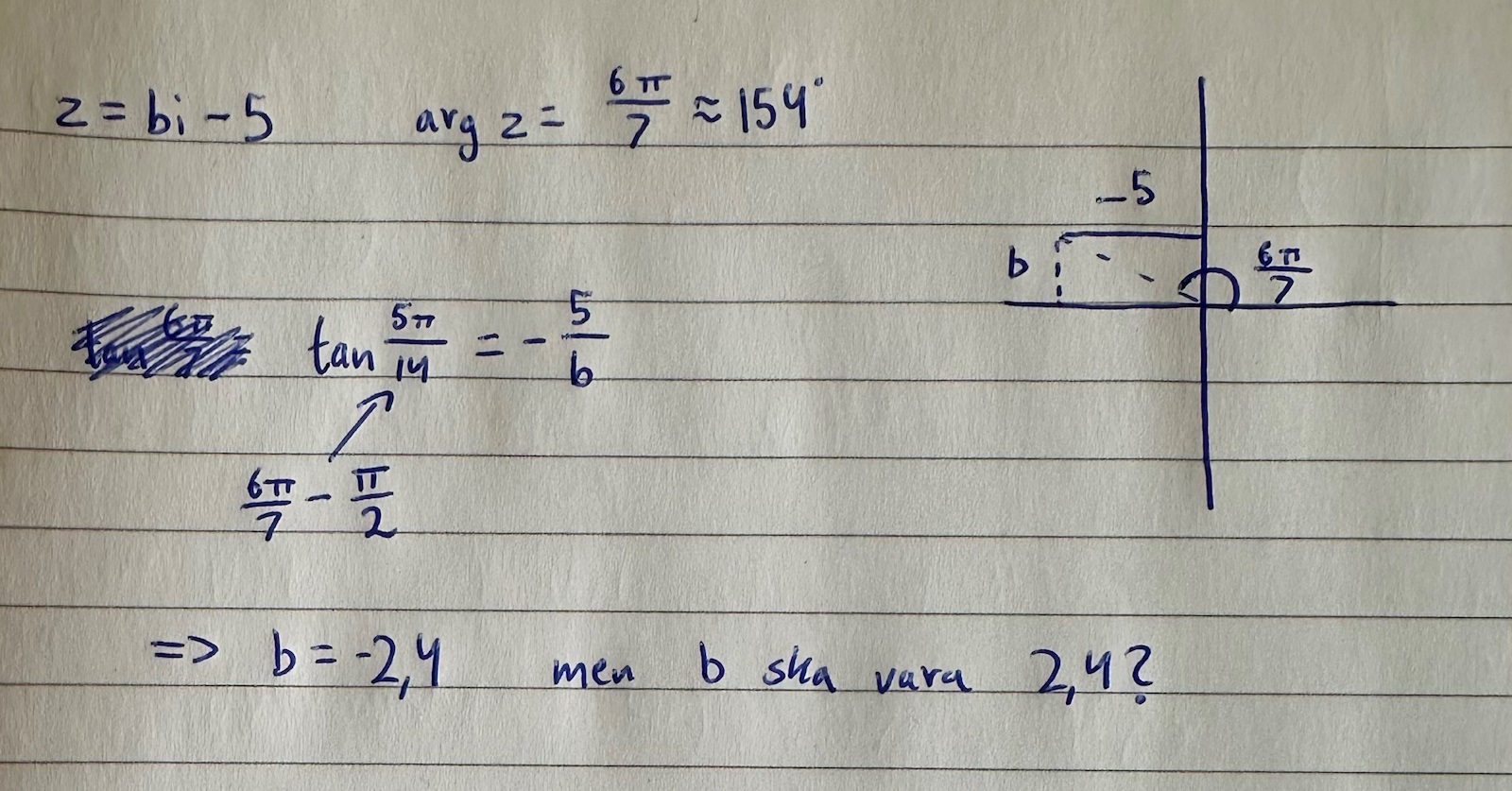
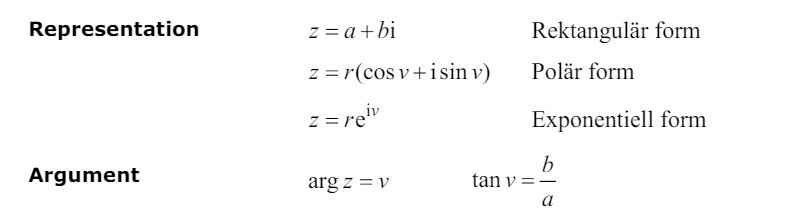
Den triangel som du riktigt räknar på kan ej ha en negativ sida. Alla sidor måste vara positiva i en triangel. Då blir den vertikala kateten positiv och rätt.
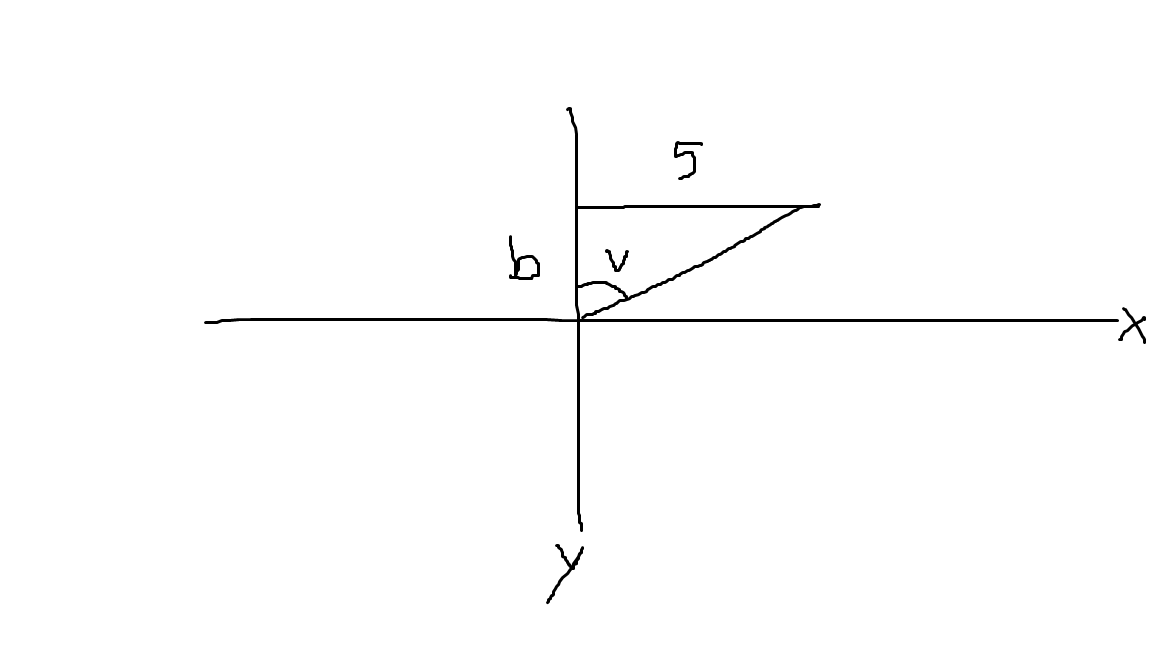
Menar du så här?
tan(x) är definierat för -♾️ < tan(x) < ♾️ medan arctan(x) bara är definierat för
-π/2 < arctan(x) < π/2.
Då är v = arctan(-b/5) = (6/7)π - π = -π/7
så att b = 5•tan(π/7) = 2,41
Då betyder du från -pi/7 till pi/7 på sista raden. Är det okej att göra så? Betyder det samma sak?
Jag kan inte se bilden som du har lagt upp.
Hoppas wikipediabilden syns nu.

Jag förstår inte hur den här bilden kopppas till frågan. Kan du förklara?
Jag hänger med nu, eftersom det är en längd på en triangel måste den vara positiv, man sätter helt enkelt längden i absolutbelopp.
Och vad som gäller formlen som står på formelbladet "tanv=b/a", känns det inte så hjälpsam eftersom den inte gäller särskilt ofta.



