Fråga 29 2014
Jag försökte lösa genom att rita upp allt och eftersom att det skärs en diagonal i rektangeln så uppstår 4 stycken likbenta trianglar, varav 2 är av samma sort. Alla "ben" sätter jag till K. Jag löser arean för triangeln med vinkeln 150grader genom areastasen och likaså för den med 30 grader. Dock är sin30=sin150, så båda har samma area. Så en triangel har arean k^2/4 och 4 stycken trianglar (som fyller hela rektangeln) ger k^2 som ska vara lika med 3 (rektangelns area). Därefter löser jag ut k med cosinussatsen. Detta ger mig 2sqrt(6+3sqrt(3))+2(sqrt(6-3sqrt(3)). Detta verkar ej vara korrekt svar, förstår ej varför.

Facit: 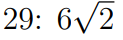
Jag tror jag löste mitt problem, men det verkade ligga i att mitt inte var förenklat men det är "rätt".
Dock din lösning, vad händer mellan tredje sista raden och näst sista?
Eftersom att våra kvadreringsregler säger att
(b+h)2=b2+2bh+h2
kan man skriva om b2+h2 som
b2+h2=(b+h)2-2bh
Detta skriver PATENTERAMERA som ett alternativt sätt att uttrycka b2+h2 på för att få ett uttryck för (b+h)2 och sedermera 2*(b+h), vilket ju är vad omkretsen är.




