fråga 18 kursprov matematik D 2011

 Punkterna A och B ligger på var sin sida av en m 30 bred kanal, se figur.
Punkterna A och B ligger på var sin sida av en m 30 bred kanal, se figur.
En kabel ska dras från punkt A till punkt B. Kabeln ska först gå genom vattnet till
en punkt P och därefter på land längs kanalens kant till punkt B.
Kostnaden för kabeldragningen är kr/m 2500 i vattnet och kr/m 1500 på land.
Bestäm vinkeln v så att kostnaden för kabeldragningen blir så liten som möjligt. (0/3/¤)
Har nån en aning om hur man kommer fram till lösningen?
Vi måste veta mer om hur punkterna ligger och vad vinkeln v avser. Kan du ladda upp en bild?
Välkommen till Pluggakuten prodger!
Med beteckningar enligt figuren:
1. Sätt upp ett uttryck för längden på sträckan AP. Det är ett välkänt trigonometriskt samband mellan vinkeln v, närliggande katet (30 meter) och hypotenusan AP.
2. Kalla sträckan mellan punkten tvärs över kanalen och punkten P (dvs motstående katet) för x. Det är ett välkänt trigonometriskt samband mellan vinkeln v, motstående katet x och närliggande katet (30 meter).
3. Avståndet mellan punkten P och punkten B är ju då 75 - x meter.
4. Nu har du uttryck för avstånden AP och PB. Sätt upp ett uttryck för kostnaden att dra kabel. Det är en kostnad per meter för sträckan AP och en annan kostnad per meter för sträckan PB. Denna totalkostnad blir en funktion av variabeln v.
5. Minimera kostnadsfunktionen med hjälp av din favoritmetod.
Även om det ser vackert ut att ställa upp kostnaden som funktion av vinkeln v, ger det en derivata som kan vara svår att bemästra, särskilt om man går på gymnasiet.
Enklare är att utnyttja för kostnadsfunktionen
Minimera kostnadsfunktionen map på x. Slutligen erhålls v ur sambandet
Lite enklare med PB=75-x. Då ska man minimera 2500*sqrt(x^2+900)+1500*(75-x). Derivering ger 2500x/sqrt(x^2+900)=1500, alltså x^2+900=25x^2/9, alltså 16x^2=8100, alltså x=22,5. Sen är v=arctan(x/30)=arctan(3/4), alltså minsta vinkeln i den välkända 3,4,5-triangeln.
Tack allihopa för era svar! Lyckades tillslut lösa uppgiften med hjälp av er :)
Hej,
Jag undrar varför alla i denna tråd föreslår att funktionen ska minimeras; digitala hjälpmedel får ju användas, så det borde inte vara något problem.
Funktionen ser då ut såhär:
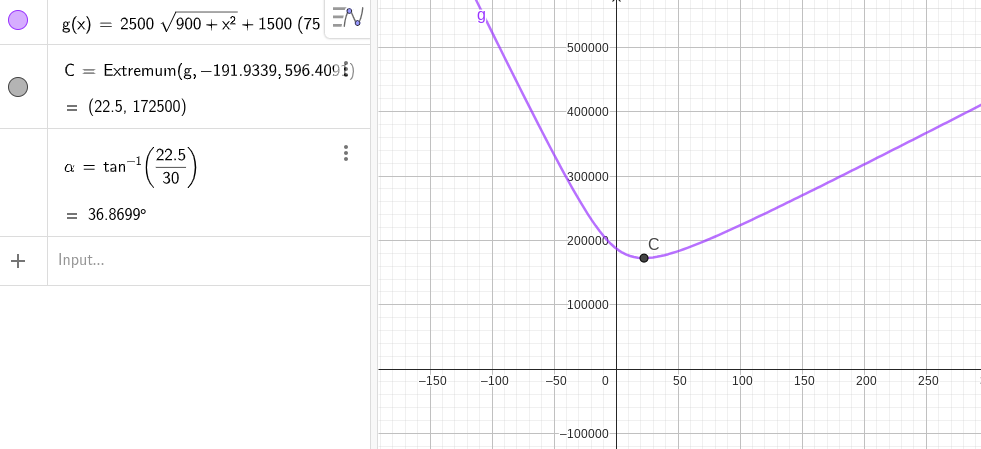
Där svaret blir ungefär 37 grader, eller är det något i uppgiften som jag missförstår?
Tack på förhand.



