Fourierserie för f(x)=-1

Jag har från uppgiften att $-1=\sum _{n=1}^{\infty }{C}_n·\sin \left(nx\right)$ på intervallet [0,π].

För att hitta C_n vill jag använda det generella uttrycket $C_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f\left(x\right)·\sin \left(nx\right) dx$ för f(x)=-1.

Jag tänker att det blir (eftersom sinus är en udda funktion) $C_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }(-1)·\sin \left(nx\right) dx=0$.

I lösningsförslaget står det däremot:

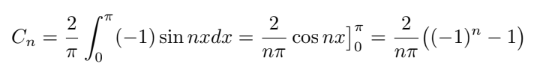
Var tänker jag fel? Är det så att f(x)=-1 är udda och att $f\left(x\right)·\sin \left(nx\right)$ då blir jämnt? Hur vet jag i så fall att f(x)=-1 är en udda funktion?