Förstår inte förklaringen? (Matematik/Matte 1/Algebra)

Vad händer med täljaren om B dubbleras? (Jätteenkel fråga)

Vad händer med nämnare om B dubbleras?

Man får 2B/2B + 1 men jag förstår bara inte hur jag ska motivera mitt svar om varför A blir större om B dubblas. Är det att jag ska säga att täljaren och nämnaren behåller samma skillnad men blir starkare vilket gör att A blir närmare 1?

När B=1 så är A=1/2. Den där termen +1 har stor betydelse. Om B=999999 så är A=999999/1000000, alltså nästan =1. Termen +1 får mindre betydelse ju större B blir och A kommer att närma sig 1.

Absolut, men det svarar väll inte på frågan om A blir större eler mindre om B dubbleras?

Charlieb skrev:
Absolut, men det svarar väll inte på frågan om A blir större eler mindre om B dubbleras?

https://mathb.in/78628

Självklart, men ett generellt resonemang krävs för att få full-pott. Hur motiverar man med ett generellt resonemang? Jag förstod även inte denna matte i exemplet, det är högre än matte 1 nivå.

Charlieb skrev:
Självklart, men ett generellt resonemang krävs för att få full-pott. Hur motiverar man med ett generellt resonemang? Jag förstod även inte denna matte i exemplet, det är högre än matte 1 nivå.

"Lösningen" består av tricket att addera 0 i formen av +1-1 i täljaren och skriva om bråket.

Olikheter hanterar man väl i Ma1. Det är högstadiematematik.

Du kan redan stanna på hälften, då 1/(2B+1) är mindre än 1/(B+1) varför du subtraherar mindre, varför det blir "mer över" i fallet med "2B".

Vad menas med B>0? Ska betyda något?

Det betyder att B. är ett positivt tal

https://www.matteboken.se/lektioner/matte-1/funktioner/olikheter-och-linjara-olikheter#!/

Ni kanske inte har kommit dit än.

Jo, nu minns jag att vi gjorde likheter/olikheter. Men vad har faktumet att B är ett positivt tal för betydelse i denna kontext, alltså för att motivera om A blir större eller mindre om B dubbleras, det står i frågan att B är positivt.

Jag förstår också inte hur det går att göra om bråket till 1- 1/B+1

Vad skulle du svara om du fick uppgiften "förenkla $1-\frac{B}{B+1}$ "?

Ahh, nu ser jag. Men mina frågor är:

För att få full pott på denna fråga behöver man motivera med ett generellt resonemang. Skulle det vara ett generellt resonemang? Att då visa att A2>A1

Jag undrar även, vad har faktumet att B är ett positivt tal för betydelse i denna kontext? Alltså för att motivera om A blir större eller mindre om B dubbleras, det står i frågan att B är positivt.

Charlieb skrev:
Absolut, men det svarar väll inte på frågan om A blir större eler mindre om B dubbleras?

Jo, det tycker jag nog:

B=0 -> A=0
B=1 -> A=1/2 = 0,5
B=2 -> A=2/3 = 0,666...
B=3 -> A=3/4= 0,75
B=4 -> A=4/5 = 0,8
... så när B går mot oändligheten, blir större, så kommer A att närma sig 1.

Detta eftersom +1 i nämnaren blir en försvinnande liten del av B, så A kommer att närma sig B/B (alltså =1).

Men, det finns många sätt att resonera på.

Yes, men jag söker efter hur jag resonerar på denna fråga. Jag vet att A ökar om B ökar.

För att få full pott på denna fråga behöver man motivera med ett generellt resonemang. Skulle det vara ett generellt resonemang? Att då visa att A2>A1 . Om inte, vad är ett generellt resonemang?

Jag undrar även, vad har faktumet att B är ett positivt tal för betydelse i denna kontext? Alltså för att motivera om A blir större eller mindre om B dubbleras, det står i frågan att B är positivt.

Charlieb skrev:
Jag undrar även, vad har faktumet att B är ett positivt tal för betydelse i denna kontext? Alltså för att motivera om A blir större eller mindre om B dubbleras, det står i frågan att B är positivt.

Därför att resonemangen inte håller för B<0.

När B närmar sig -1 "från höger", går A mot -∞.

Sedan, när B går från -1 "åt vänster" kommer att att gå från +∞ mot +1.

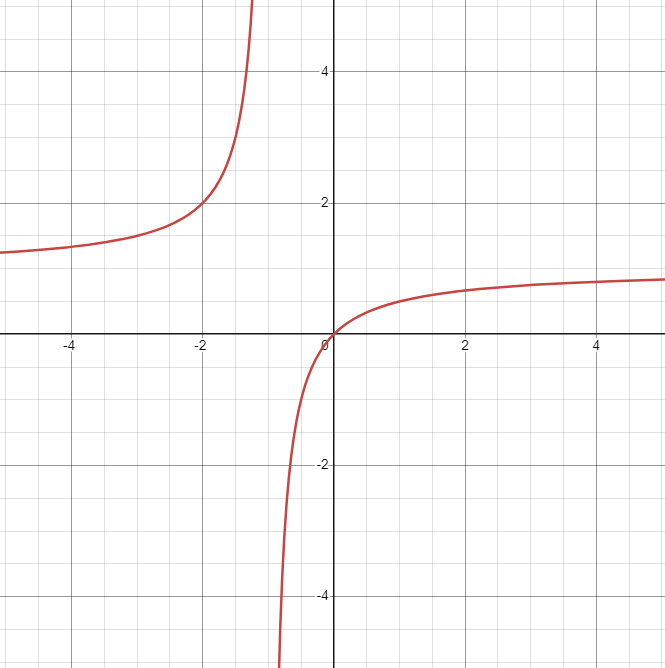
Tack!

Är du supernyfiken, så kika på:

Det är precis vad den här uppgiften handlar om.

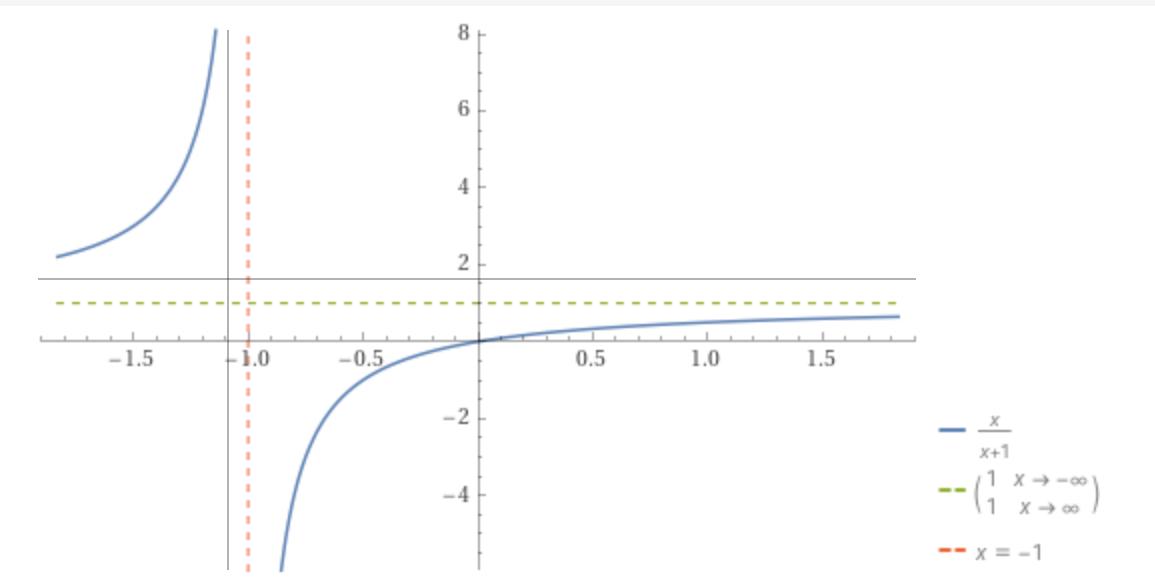
Svar på mina frågor i inlägg 2 är

Om B dubbleras blir täljaren dubbelt så stor.
Om B dubbleras blir täljaren större, men inte dubbelt så stor.

Då ser man att A blir större. 2/k blir ju mer än 1, när k ligger mellan 1 och 2.